This is Volume X of XII – Reasoning Power or Practical Logic

 

Personal Power Series:

Volume I. Personal Power or Your Master Self

Volume II. Creative Power or Your Constructive Forces

Volume III. Desire Power or your Energizing Forces

Volume IV. Faith Power or Your Inspirational Forces

Volume V. Will Power or Your Dynamic Forces

Volume VI. Subconscious Power or Your Secret Forces

Volume VII. Spiritual Power or The Infinite Fount

Volume VIII. Thought Power or Radio‑Mentalism

Volume IX. Perceptive Power or The Art of Observation

Volume X. Reasoning Power or Practical Logic

Volume XI. Character Power or Positive Individuality

Volume XII. Regenerative Power or Vital Rejuvenation

 

Volume X – Reasoning Power or Practical Logic

 

Practical Logic
The Psychology of Reasoning
The Law of Logical Analysis
The Law of Logical Synthesis
The Law of Logical Judgment
The Law of Logical Analogy
The Law of Logical Induction
The Law of Logical Causation
The Law of Logical Deduction
Some Practical “Points”

 

 

 

Practical Logic

In This book you are asked to consider that wonderful phase of Personal Power known as Reasoning Power, and to include in such consideration the principles of Practical Logic. In the practical instruction which is set forth in the series of books of which the present volume is one, Personal Power is regarded as being a phase of the expression and manifestation of POWER, i. e., the All-Power from which all forms and phases of particular Power directly or indirectly proceed.

Reason is the activity of the highest faculties of cognition, thought, understanding and knowledge. It is the highest process of the intellect, the thinking faculty, the faculty of understanding, the faculty of knowing. Reasoning proceeds by logical processes, even when the reasoner knows naught of formal rules of Logic. Logic is: “The science or art of exact reasoning, or of pure and formal thought; or the laws according to which the processes of pure thinking should be conducted.” Logic may lie regarded from either of two general viewpoints, viz., (1) that of Formal Logic, in which the subject is treated in accordance with the academic, technical, formal position; or (2) that of Practical Logic, in which technical form and academic treatment are largely set aside in favor of the presentation concerned with efficient use, employment, work, utility and action. In the present consideration there shall be but little reference to the methods of Formal Logic; the subject will be presented almost entirely according to the methods of Practical Logic.

Reasoning applied according to the methods of Practical Logic, consists of the processes of consecutive thinking in which the mind passes before it in review the essential facts concerning a subject, and then, after a careful consideration of their respective characteristics and relations, draws conclusions and makes judgments conformable with truth. Reasoning, and Practical Logic, are concerned with the discovery of the truth regarding the existence, nature and character of any subject or object of thought to which the attention is directed for that purpose; moreover, they are concerned with the discovery of efficient means whereby definite ends may be secured, and definite results effected.

One of the distinguishing characteristics of Reasoning according to the methods of Practical Logic may be expressed by the term “purposive effort,” i. e., effort directed definitely and with purpose. Reasoning inspired by Practical Logic must ever be purposive—it must have an aim and end, an intention, object and purpose, and must be inspired and directed by these motives. That aim and end, intention, object and purpose of Reason and Practical Logic is always found to be: the discovery of truth and of facts.

When you reason about anything, you do so in order to discover something at present unknown to you. That which you seek is unknown to you, though usually you have a more or less general notion of the direction which the mind must travel in its search for it. You may not know just what you want, or just what you hope to find; but you are conscious of the want of a general or particular “something,” and you have a more or less definite idea of the general class of things to which it belongs, and in which it must be sought. The more clearly and definitely you perceive the exact nature of the want, the more definite and determined will be your reasoning leading up to its discovery. It has been well said that, “All reasoning begins in doubt”; that “the process of reasoning is always one of problem solving; the occasion for reasoning is always a ‘thwarted purpose’.”

If you were Omniscient—All-Knowing—(as the Absolute or Supreme Being of philosophy and theology always is held to be), then you would never have any need of reasoning, and, consequently, would never reason at all. This, because in such case you would have nothing left about which to reason—you would know all things. Your purpose would never be thwarted, for there would be nothing to thwart it, and nothing by means of which it might be thwarted. You would never be perplexed about anything whatsoever, and would never have to “think out” or “think about” anything.

Philosophers have held that an Omniscient Omnipotent Being can not properly be held to “think” at all in the form of reasoning; such a Being would transcend Reason—it would “know” everything that is to be known, without effort, directly and immediately; moreover, it would have no “thwarted purpose” to overcome and remedy by means of Reasoning. Reasoning, then, is seen to be a mental power reserved for finite beings who have much to learn, and many “thwarted purposes” to overcome and to remedy—and who need to employ reasoning in order to cure such troubles and to remedy such deficiencies. Reasoning Power, then, is seen to belong to the category of Personal Power.

Logic investigates the processes of Reasoning in order, (1) to discover the qualities distinguishing correct thinking; and (2) to formulate rules and methods whereby invalid thinking may be avoided, and valid thinking may be secured. It announces certain basic laws and principles which have been found to govern all valid thinking; it teaches certain rules and methods by means of which valid thinking may be insured and secured, and invalid thinking avoided.

Formal Logic strives to give to the form of Logical Reasoning the technical, scientific accuracy of mathematical formulas; its teachers have sought to discover and announce logical terms and formulas, often of extreme technicality and complexity, which correspond to those employed in higher mathematics. Practical Logic, on the contrary, holds that only in a very inadequate way can Logic be reduced to algebraic expression; its teachers seek rather to announce plain, practical rules and methods whereby the average thinking individual may assure himself that he is pursuing the correct general laws and principles of Reasoning, and that he is avoiding the fallacies which beset the road of thought.

As we have already told you, we shall have very little to do with Formal Logic in this book; but we shall have much to do with Practical Logic. We shall proceed upon the theory that, “Psychology is descriptive; Logic is regulative and corrective; Reason is creative.” The edifice of our instruction is built upon sound foundations, having a strong pillar at each corner. These foundation pillars are as follows, (1) Psychology, (2) Practical Logic, (3) Experience, and (4) Common Sense. Each pillar has its definite and particular place and purpose in the whole plan; but no one of them would be strong enough to support the structure were the other three removed. It is only when the four elements represented by these pillars are united in strength, and harmony of arrangement, that the structure is properly supported and scientifically balanced.

You probably have desired (at some time in your life at least) to learn something concerning the principles of Practical Logic or Logical Reasoning. Most persons have felt this desire. Many persons have sought such information in the technical textbooks of Formal Logic; but most of them have found in such books chiefly a great disappointment. Instead of practical instruction, they have found strange, mysterious terms. Instead of practical rules, they have found abstruse, artificial formulas having apparently no relation to everyday life and thought and their requirements. They have asked for the bread of instruction, and have been given the cold stone of formal, technical, academic categories, and hair-splitting distinctions having no discernible connection with the actual thinking processes of the average man. Many an eager seeker after the truths of Logical Thinking has become discouraged after an experience of this kind—possibly after several such—and has given up all hopes of ever learning anything about the real meaning and use of Logic.

But, we are glad to be able to say, there has been of late years a decided tendency in the direction of bringing down the subject of Logic from the region of thin air and extreme coldness in which it has been kept for so long—down to the warmer and more comfortable valleys wherein most of us dwell. Formal Logic is taking its place with the study of the “dead languages”; Practical Logic is taking a place on the level with the study of the living tongues. The pragmatic spirit of modern thought is insisting that the essential, usable, workable elements of Logic be separated from its ancient dead forms, and be made obtainable in living, practical forms adapted to the requirements of everyday life. Practical Logic is “coming to the front,” while Formal Logic in many cases is being “shown out by the back door” of practical mental establishments.

It has been said that, “The theory of every operation of the mind is later than its performance; men were accustomed to think correctly long before they began to reflect upon their thinking faculties and the processes by which their results were obtained.” It has also been said that, “A meagre soul can never be made fat, nor a narrow soul be made large, by merely studying the Rules of Thinking.” So, have your thinking first, and plenty to think about, and then ask your logician to teach you how to scrutinize with a nice eye the processes by which you have arrived at your conclusions.

The real office of Practical Logic is largely corrective and regulative. It points out and corrects fallacious reasoning on your part; it enables you to detect fallacious, sophistical, or casuistical reasoning on the part of others; it exercises a direction over your habitual processes of thought, thereby inhibiting illogical forms of thought and supplanting them by true logical forms. If it simply enabled you to detect the false reasoning of other persons, and to prevent you from being deceived by such, the study of Practical Logic would be well “worth while”; in reality, it not only accomplishes this task, but also performs other equally important work for the individual who earnestly studies its principles.

There are many persons who have never even heard of the rules and methods of Logical Reasoning, and who do not know even the meaning of the principal terms employed in that science, but who, nevertheless, have really been employing these methods with more or less correctness, and observing these rules more or less faithfully, during their entire period of life. They are like the man in the French comedy who expressed surprise when informed that he had been “talking prose” all his life, for (said he) “I never learned prose, never studied it, never was taught it—never even knew that I was talking it; I must have a remarkable mind!” So, many would doubtless wonder if informed that they were using logical forms and methods in their thought; they, too, might think their minds to be wonderful, inasmuch as they had never studied Logic and never know that they were employing its methods with more or less success.

Jevons says: “Ninety-nine people out of a hundred might be surprised on hearing that they had been employing syllogisms and other logical forms, converting propositions, framing hypotheses, and making classifications with genera and species. If asked whether they were logicians, they would probably answer, No! They would be partly right; for I believe that a large number even of educated persons have no clear idea what Logic is. Yet, in a certain way, every one must have been a logician since he began to speak. I may be asked: If indeed we cannot help being logicians, why do we need Logic at all? The answer is that there are logicians and logicians. All persons are logicians in some manner or degree; but unfortunately, many persons are bad logicians, and suffer harm in consequence. It is just the same in other matters. * * * We must reason well or ill; but Logic is the Science of Reasoning which enables us to distinguish between the good reasoning which leads to truth, and the bad reasoning which leads to error and misfortune.”

The logicians did not invent the essential forms of Logic; instead, they discovered them already in existence and being employed with more or less accuracy and precision by all thinking individuals. The laws of Logical Thought are not commands announced by some ruling authority; they are merely statements of “the way the mind works” when it reasons truly and efficiently; they are Laws of Nature, not laws of men. The Laws of Practical Logic are simply the statements of certain principles and methods observed and applied, more or less faithfully and consistently, by intelligent men and women when they reason seriously, carefully, and deliberately.

Men reasoned more or less correctly, observing more or less faithfully the essential logical forms, long before the term “Logic” was coined, and still longer before the present-day principles and methods of Logic were announced. This, however, is no more remarkable than the fact that all Nature, and all contained within Nature, obeyed the Law of Gravitation long before that law was discovered, and still longer before its principles of operation were generally and commonly known to men. Newton simply discovered the existence of certain physical laws—and announced them; logicians simply discovered the existence of certain mental laws—and announced them.

It is true that men have done good thinking without a formal acquaintance with the Laws of Logical Thought; but they did so “in spite of” their lack of knowledge—not “because of” it. No man ever thought efficiently because of his ignorance of the principles of Logic! On the other hand, you can no more reasonably expect to become a proficient and efficient logical reasoner by merely knowing the laws of Practical Logic, than you could expect to become a proficient and efficient mathematician by simply knowing the Laws of Mathematics. In either case, something more is needed; but in each case it is equally true that you will do well to learn thoroughly those rules, principles, and laws in order to attain correctness, to secure freedom from error, and to detect the errors of others which are often claimed to be truth, in these respective branches of scientific thought.

In the spirit of the above statements, the following instruction in the principles of Practical Logic is offered to you.

The Psychology of Reasoning

Psychology does not attempt to solve the problem of “just what Mind is.” Instead, it contents itself with regarding Mind as experiencing “a series of mental states,” and of discovering and announcing “just how” the mental processes arise, proceed, and manifest themselves. In this way, Psychology inquires into the mental processes involved in the activities of Reasoning, and reports just what laws, principles, and methods of procedure it has discovered to be active in that important field of mentation.

In the first place, it discovers and reports that Reasoning is a phase or form of Thinking; that phase or form which is concerned with considering, deliberating, forming opinions, judging, concluding and ascertaining valid grounds for belief in anything. It discovers and reports that Thinking employs Thoughts as its material, these Thoughts being combined, woven and manufactured into the complex products of Reasoning.

Perception and Percepts Thoughts are of varying degrees of complexity, ranging from the simplest perception to the most complex general idea. The simplest form of Thought is that known as the Percept, or the simple idea derived from Perception. But even the simplest Percept is really complex, and composed of several elements, as you shall see presently. Perception is not the simplest and most elementary mental process; below it in the scale is what is known as Sensation. Sensation, however, is not usually included in the category of Thought; on the contrary, it is considered to be “the raw material of Thought.” It is worth while to pause here a moment in order to note the distinction between Sensation and Perception.

Sensation is: “The mental state arising from the excitation of portions of the nervous system by reason of their contact with objects or forces external to the nervous system.”

Perception is: ‘”The mental state arising from (1) the conscious recognition of the sensory reports; (2) the interpretation of these reports as particular kinds of Sensation: and (3) the association of these reports with the external object or force originally giving rise to them.

Example: There is placed before you a certain external object—the object known to most persons as an Orange. Your mental processes concerning it are as follows: Your sense of Sight reports certain conditions arising from an excitation of the optical nerves; your sense of Touch reports certain conditions arising from the contact of the nerves of your finger-tips with something external to it; your sense of Smell reports certain conditions arising from the contact of your nerve-ends located in the mucous membrane of your nostrils with certain subtle emanations of the substance of something external to them; your sense of Taste reports certain conditions arising from the contact of the nerves located in your mouth and tongue with an outside substance which has been placed within the mouth, or upon the extended tongue; your sense of Hearing makes no report in this particular case.

Your Perception then proceeds to recognize and interpret these Sensations; in doing so, it is aided by your past experience with Sensation, by means of which you have evolved from the simple-sensation stage of the young infant to the perceptive stage of the adult of at least average experience with external things. Your Perception also proceeds to associate these Sensations with things external to itself. It recognizes and interprets these sensory reports in terms of perception of size, shape, form, distance, color, etc.; in terms of perception of weight, size, shape, form, degree of hardness, etc.; in terms of perception of odor, fragrance, aroma, etc.; in terms of sweetness and agreeable taste, etc. To all of these sensory reports it applies certain terms which it has adopted as representing certain perceived sensations. It recognizes the perceptive elements of roundness, certain size, certain shape, certain form-characteristics, yellowish color; of certain weight and certain “feel”; of fragrance and aroma; of sweetness and pleasant taste. It interprets these perceptive elements in symbolic forms of thought and speech called “words,” or “terms.” It associates these perceptive elements or characteristics with the external object which has given rise to the several sensory-stimuli in question.

You may object that you “perceive” instinctively, and that you never perform consciously the processes just described. But we would remind you that while Sensation is instinctive, Perception is acquired through experience, and becomes instinctive only by reason of repeated practice and cultivation of the habit. The young infant “senses,” but does not “perceive.” It learns only by experience to distinguish between its various sensations; to recognize them as such; to interpret them; to associate them with external objects. It “feels” from the start; but it must learn by gradual experience to recognize, interpret, and associate with external objects, such feelings and sensations.

Sully gives us a simple, effective figurative illustration of the difference between Sensations and Perceptions. He says: “Sensations are the alphabet by which we spell out the objects presented to us. In order to grasp and apprehend these objects, these letters must be put together after the manner of words. Thus the apprehension of an apple by the eye involves the putting together of various sensations of sight, touch and taste. This is the mind’s work, and is known as Perception.” He further tells us that by these Sensation-letters we may spell out, and make up Perceptive words; for instance, from the several Sensation-letters of O, R, A, N, G, E, we may spell out and make up the Perceptive-word “ORANGE.”

Gordy also gives us a practical explanation, as follows: “What does the mind do with its sensations of colors, odors and tastes in order to perceive colors, odors and tastes as qualities of objects. It groups them together, does it not? When you look at an apple, you group its color, taste, and smell together as qualities of one object. * * * You perceive only when they seem to be qualities actually forming a part of the objects in the world about us, or states of our own bodies. * * * Strictly speaking, what we do when we perceive is to make a group consisting of one or more sensations, and ideas of sensations, and to regard the group as qualities of an external object.”

A Percept is: “A Thought in which one or more sensory elements are recognized, interpreted, and associated with an external object; are regarded as being qualities of that object; and are incorporated into a group, giving the impression of a single and unitary whole, which is regarded as constituting the idea and meaning of that object.” Illustration: When we perceive an external object, e. g., an Orange, we experience a group or aggregate of sensory impressions which by recognition, interpretation and association we combine into the unitary, single Thought of “that Orange.” (Not an Orange, or any Orange, however, but merely and strictly “that particular Orange”; the “an” and “any” being an element of another class of Thoughts).

Conception and Concepts The form or phase of Thought which is immediately above the Precept in the scale of Reasoning is known as the Concept, or the complex idea derived from Conception. The Concept is constituted, composed, and made up of several Percepts. Just as the Percept represents the Thought of the composite qualities of a particular object, so does the Concept represent the Thought of the composite essential and common qualities of a certain class of objects. Thus, we have found that the Percept of “that Orange” is a composite of the qualities of that particular Orange; now we find that the Concept of “Orange” (meaning any and every Orange—all Oranges) is a composite of the qualities which are possessed in common by all Oranges, and which each and every Orange must possess in order to be “an Orange” at all—all the essential qualities of Oranges in general—all the qualities which must be stated in a complete definition of the general term, “Orange.”

Conception is: “The mental act of combining perceptive ideas into a more general group-idea of a general class of, objects; by it is formed the Concept, or the Thought or idea representing the whole number of objects denoted by the several general perceptive ideas composing it.” To understand the process of Conception more clearly, you must first understand the essential nature and character of the Concept which is formed by the act of Conception. We ask you to give careful attention to the following consideration of the Concept, for you must understand this thoroughly if you wish to manifest efficient Reasoning Power along the lines of Practical Logic.

The dictionary definition of Concept is: An abstract general conception; a general notion; a universal idea; the idea or a larger or smaller class of particular things.” In traditional Logic, the Concept is, “The idea of a characteristic or characteristics belonging to more than one person or thing and, thus, to a general class of things; it stands opposed to the Percept which is an idea dealing with particular things only.”

The act of Conception consists of several stages or phases, which are always performed with greater or less precision and accuracy by the person “thinking,” although he may not be conscious of their nature or of the order observed in their manifestation. Having acquired only gradually the art of performing this process; having obtained it along the lines of the evolution and development of his mental activity from early childhood; and having taken on the habit of performing it, he employs it more or less unconsciously, and he takes it for granted. Analysis, however, will show that these stages or phases are necessary, and that they are always performed consciously or unconsciously by the thinking individual.

The processes above referred to are as follows: (1) Perception of numerous particular objects; (2) Comparison of these particular objects, and noting wherein they agree or differ in their qualities; (3) Selection of certain individual objects which are found to agree in definite fundamental qualities— to be “similar” or “alike” in certain respects; (4) Generalizing, or classifying these similar or “like” objects into classes, which classes have as their essential and necessary qualities those characteristics which have been discovered to be common to and universal among those selected individual objects; (5) Denominating or giving a name or applying a term to that general class of objects—putting a verbal tag or label on it to distinguish it as a whole.

Thus the general class of fruit known as “The Orange,” or “Oranges,” includes all the fruit of that general kind; and its class-qualities are those which are essential and necessary to all Oranges, and which are common and universal among all Oranges, though the numerous particular Oranges may differ materially in non-essential characteristics. The Thought, Idea, or Notion of “The Orange,” or “Oranges” (as a class) is the Concept “Orange,” to which that general term is applied. Into that class must fit, and under that name or term must fall, each and every one, any and all, of the fruit known as Oranges.

Gordy says: “Conception is that act of mind by which it forms an idea of a class, or that act of mind that enables us to use general names intelligently. * * * We never see a class (i. e., an indefinite number of individuals that resemble each other in certain particulars). Classes do not make themselves known to us through any of the senses. How then does the mind form an idea of a class? To answer that question is to state what the mind does in Conception.”

Smaller Concepts may be combined into larger ones, by the application of the characteristic principles of Conception, viz., (1) Cognition of several particular Concepts; (2) Comparison of one particular Concept with another or others, for the purpose of noting resemblances and differences; (3) Selection of certain particular Concepts which are found to agree or resemble each other in one or more particulars; (4) Generalizing or classifying these “like” Concepts into larger Concepts; (5) Affixing names and terms to these larger Concepts.

The process of Conception may be continued at great length, higher and still higher generalizations being made. The end comes only when you have generalized every existing object into one supreme and universal class—the Summum Genus- comprising either all existing things regarded as a whole, or the ultimate essence or substance of such. To this Ultimate Concept is given the class term or name, “Being,” the sole essential and necessary quality of which is Existence in some form, phase, mode or degree of Being-ness—a Something or Somewhat of which the only essential quality is that “It exists.”

Besides the quantitative distinction between different kinds of Concepts, i. e., the difference consisting of the number of objects included in their content, there is to be noted a qualitative distinction, i. e., a difference in general kind, character, or quality. The several most important kinds of qualitative differences between Concepts are based upon the following lines of distinction: (1) Material Quality, (2) Incidental Quality, (3) Causal Quality; each of these are considered below in further detail.

The material quality of a Concept is determined by the fundamental material character of the objects represented in the general idea, considered apart from their incidental relations or associations with other things. Example: The Concept “Sheep” is formed and composed of the essential and necessary fundamental qualities common to and universally present in the entire number of particular objects called “sheep”; this apart from any use or employment of sheep, or any part or portion of their bodies, their energy, etc. In the same way, following the same rule of qualitative unity of character, the Concept “Sheep” may become a part, element, or factor in the larger Concept called “Ruminants.” Likewise, the latter Concept may be included in the still larger one of “Mammals”; and this, in turn, into a still greater one called “Animals”; and so on, until the Ultimate Concept of “Being” is reached.

The incidental quality of a Concept is determined not by the fundamental material character of the objects represented in the general idea, but rather by their incidental relations or associations with other things—certain subordinate or secondary qualities. The most important incidental qualities of this kind are those concerned with Utility, Use, Employment and Practical Application to certain purposes or ends. Example: Things (and their Percepts) may be classified under the category of the quality of “being useful for fuel purposes”; of “being useful as light-producing agents”; of “employment as disinfectants”; of “use as medicinal remedies”; as “use for tanning purposes,” “curing purposes,” “preserving purposes,” “pickling purposes”; or use, employment, utility, or possible application for any purpose whatsoever. Under this mode of conceptual classification, Coal, Wood, Oil, Fats, etc., may be included in the Concept of Fuel (i. e., “things serving for heat-producing purposes”). In the same way, Torches, Oil, Candles, Electric-Lamps, etc., may be included in the Concept of “light-producing things.” Such examples might be extended indefinitely, but the above will serve to illustrate the characteristic element of this form of classification of Concepts.

The casual quality of a Concept is determined neither by the fundamental material character, nor by the incidental relations or associations, of the objects represented in the general idea; but rather by the power of such objects to produce casual results or effects by reason of their presence and actions. The “causal quality” of a particular thing is represented by the idea of “how does it work; what it will do; what results or effects proceed from its presence and action.” The “causal qualities” of a number of things, when found to agree in general causal character, result in their being combined and included in a Concept of a “Law.” Such a “Law” is merely the Concept embodying the general idea of “how and in what way this class of things works.” A still higher causal synthesis, or generalization, results in the Concept of a “Principle,” or “Law of Laws” of Action—a Cause of Causes. Raised to its highest power, this form of Concept posits the existence of an Ultimate Principle of Cause—a Causeless Cause.

The General Processes of Reasoning Psychology also furnishes us with a comprehensive classification of the several general processes involving in Logical Reasoning; this classification proceeds as follows:

Judgment upon the Materials of Thought, resulting from the following processes, viz.:

1. Analysis or the discovery of differences in character.
2. Synthesis, or the discovery of resemblances in character.
3. Inference, or the induction or deduction of new facts or truths from others previously discovered by Analysis or Synthesis.

The following brief statements will serve to explain in greater detail the nature and meaning of the above-mentioned several processes involved in Logical Reasoning:

Judgment is that mental process involving comparison and discrimination (i. e., discernment of resemblances and differences in the qualities of respective Percepts or Concepts), whereby the mind forms opinions and decisions concerning the nature of things under consideration. In the processes of Judgment, the mind compares its perceptive or conceptive thoughts, ideas, or notions, and then reaches a decision concerning (a) their degree of resemblance or difference; (b) their respective relations of “the whole and its parts,” or of “the parts and their whole”; (3) their respective relations of cause and effect, or effect and cause; or (4) their respective incidental relations. Judgments (when completed) are always affirmative or negative. The mind cannot reason or think logically without judging; to think or reason logically is to judge. From its simplest and most elemental stages and phases, to its most complex and derivative forms and modes, Reasoning is found to employ the processes of Judgment—it cannot proceed without them.

Analysis is that mental process whereby differences between the qualities, properties and attributes—the respective characters—of two or more objects of perception or conception are detected and discovered As a consequence of Analysis, particular Percepts or Concepts are mentally analyzed, dissected, separated, refined, or resolved into their constituent parts, elements, or factors, each of which is represented by a simpler mental idea and its appropriate term.

Synthesis is that mental process whereby resemblances in the qualities, properties and attributes—the respective characters—of two or more objects of perception or conception are detected and discovered. As a consequence of Synthesis, particular Percepts and Concepts are mentally synthesized, joined, combined, associated, related, put-together, united and fused into a Concept of a higher order, a greater class, a more general and more nearly universal character—into a greater Whole, Law, or Principle.

Inference is that mental process whereby, through Analogy, Induction, or Deduction, new facts or truths are adduced or drawn from others previously discovered by the processes of Analysis or Synthesis, or by both of these combined. It has been defined as: “Deduction or Induction from preceding known facts or premises, resulting in the discovery of new facts and truths.” Again, it has been stated as: “The process of coordinating and systematizing previously acquired knowledge, so that new knowledge is thereby gained through induction or deduction, or similar process.” Inference is the process of reasoning from the known to the unknown; or the discovery of a third fact from two facts already known. It produces a new and third Judgment based upon two prior Judgments which have been arrived at through some previous reasoning of some kind. Its forms are known, respectively, as Logical Analogy, Logical Induction, and Logical Deduction.

Note: You are requested to familiarize yourself with the above-stated explanations of Analysis, Synthesis, Inference, and Judgment; as well as of the previously stated explanations of Precepts and Concepts. A thorough understanding of these elements of Logical Reasoning, or Reasoning Thought, is essential for your comprehension of the further instruction to be presented in the following sections of this book. The fundamental building-materials of Thought, i. e., Percepts and Concepts, and the basic processes whereby such materials are put together and built into the structure of Thought: these must be understood by those who desire to engage in the working of Thought-Building, Logical Reasoning, or Rational Thought.

The Seven Axioms of Logical Reasoning

In Logical Reasoning, you are asked to apply the principles of several fundamental and basic axioms. An “axiom” is “a self-evident and necessary truth; a proposition which it is necessary to take for granted; an established principle.” These Axioms of Logical Reasoning, however, while offered as self-evident and necessary to be taken for granted, are not the arbitrary dogmas or dicta of real or pretended authority; instead, they represent the universal experience of human thought rationally applied and directed; they represent truths “of which the contrary is unthinkable, and which would constitute a scandal of rational thought.” These Axioms are in constant use, in the thought processes of reasoning human beings; they are “taken for granted,” and are either directly asserted or tacitly implied in all Logical Reasoning.

The Seven Axioms of Logical Reasoning (which we shall consider in detail in the succeeding sections of this book) are named, and briefly stated, in the following paragraphs, as follows:

1. The Axiom of Logical Analysis: “Every thing is composed, constituted and made-up of (a) parts, elements and factors, and qualities, properties and attributes, which in combination, arrangement, correlation and coordination constitute its character and make it just what it is, and into which it may be analyzed, dissected and separated in thought.”
2. The Axiom of Logical Synthesis: “Every thing belongs to a class of things possessing one or more common and essential characteristics; many things belong to several classes of different (though not opposing) character.”
3. The Axiom of Logical Judgment: “All Logical Judgment is based upon these three fundamental Laws of Thought, viz., A thing is always just what it is, and nothing else, at a given time and place, no matter what particular name or term may be employed to indicate, designate or represent it; (2) A thing cannot both be and not be just what it is affirmed to be, at the same time and place; (3) A thing must either be, or not be, that which it is affirmed to be, at a given time and place—there is no third alternative.
4. The Axiom of Logical Analogy: “A few things which are alike in many respects, are probably (though not certainly) alike in some other respects.”
5. The Axiom of Logical Induction: “What is discovered to be true of a great number of observed objects, things, or individuals of a definite general class, is practically certain to be true of that general class as a whole; the characteristics assumed to be possessed in common by all the individual objects or things in a definite general class, constitute the accepted essential characteristics of that class as a whole.”
6. The Axiom of Logical Causation: “Every change, happening, event, or entrance into or exit from existence, proceeds from precedent conditions or causes; given the same causative factors, the same material elements, and the same environmental conditions, the same results and effects will follow in all cases so determined and conditioned.”
7. The Axiom of Logical Deduction: “What is true of the class as a whole must be true of each, every, and all of the individuals composing that class.”

Note: You are advised to commit to memory the above-stated Seven Axioms of Logical Reasoning. A consistent and intelligent application of their respective principles will open to you many doors of the Temple of Logical Thought.

The Law of Logical Analysis

You are now invited to consider that important Law of Logical Reasoning known as the Law of Logical Analysis.

This Law represents the universal experience of human thought rationally applied and directed. The Law of Logical Analysis is expressed in the first of the Seven Axioms of Logical Reasoning, which is as follows:

1. THE AXIOM OF LOGICAL ANALYSIS: “Every thing is composed, constituted and made-up of (a) parts, elements and factors, and (b) qualities, properties and attributes, which in combination, arrangement, correlation and coordination constitute its character and make it just what it is, and into which it may be analyzed, dissected and separated in thought.” This axiom states a truth which is verified by all human experience, is supported by the common-sense reports of the race, and is substantiated by the judgment of the keenest logical and philosophical thought; It is to be regarded as a self-evident truth, and as a proposition which may be taken for granted; it is assumed in all logical thought, and is implied in all true reasoning. The following consideration is not intended to be offered as proof of its truth; but is designed merely to elucidate and make clear the manifestation of this principle in the world of thought and things.

Our consideration properly begins with a definition of the term “Thing,” as employed in this axiom. Let us come to an understanding of the meaning of this important term; by so doing we reduce the risk of misunderstanding in the course of this instruction. Inasmuch as the greater part of all disputes arise from misunderstanding of, and non-agreement upon, the principal terms employed in the reasoning, it is important that an agreement of this kind be reached at the beginning of an argument or other process of reasoning. This will serve to explain the frequent resort to definitions which you will discover in the course of this instruction.

A “Thing” (in the present usage of the term) is: “Any separate and distinguishable object of thought.” The term “separate” (as employed in this definition) means, “distinct, apart from others”; the terms “distinguishable” (as employed in this definition) means, “capable of being set apart from others by visible marks, signs, or characteristics; or, capable of definition of terms, or logical division.” A more technical definition of “Thing” is: “Whatever exists, or may be conceived to exist, as a separate, concrete entity, or as a specific, particular object of thought.” In this category of Things are contained all objects of which we have, or can have any practical knowledge through the senses, or through thought employing the material furnished by the senses. If there are any entities outside of this category, we do not and cannot know them in the way in which we know the things of ordinary experience.

Parts, Elements, and Factors Now for the definitions of the three terms employed in that clause of the axiom following the symbol “(a)”, viz., “parts, elements, and factors.” A “Part” is: “A constituent portion of a whole; a portion less than the whole of a thing.” An “Element” is: “One of the essential parts or principles of which anything is composed, and upon which its distinctive character is based.” A “Factor” is “One of the elements of a thing, which when multiplied or combined constitutes that product which is the whole of the thing.”

It will require but little thought on your part to convince you that everything you have ever experienced, or can imagine yourself as experiencing, is “composed, constituted, and made up of parts, elements, and factors,” and is subject to physical or mental analysis into such. You can form no idea of a concrete, definite thing as being devoid of “parts, elements or factors”; your imagination, as well as your reason, will find itself unable to form a conception of such a thing for you. Even if you were to find yourself able to conceive of such a thing, you would not be able to find words and terms with which to express the thought.

The principle of composition and analysis is illustrated by the ancient Buddhistic story of the dialogue between a sage and the king who was visiting him. The sage asked the king: “What do you mean when you think or speak of your chariot?” The king replied: “When I think or speak of my chariot, I mean my vehicle which is composed of the body, the wheels, the axle, and the pole.” Again the question was asked: “What do you mean when you think and speak of a river?” The answer was: “When I think and speak of a river, I mean its flowing water, its bed, and its bank.”

The sage then asked the king: “Do the body, the wheels, the axle, and the pole of the chariot, taken apart from one another, represent your thought and idea of a chariot? Do the flowing water, the river-bed, the river-banks, taken apart from one another, represent your thought and idea of a river?” The king replied: “Nay, reverend sir; these things, apart from one another and not joined together, are naught but separate and distinct things, and when in that condition constitute neither the chariot nor the river; in such case there is no chariot and no river to be perceived and known to my mind.”

Then asked the sage: “Can you think of a chariot or of a river without including in your thought these parts which constitute it?” “Nay, sir; I cannot think of either chariot or river in this way; when I attempt it I find myself thinking of nothing, or of a mere word or name.” “Then,” said the sage, “can you think of a chariot or a river by thinking merely of the separated parts which when combined constitute them?” “Nay, reverend sir,” replied the king, “when I try to do so I find myself thinking merely of separate and disconnected parts, and not of the chariot or the river at all; in such case, as before, I find that to me the chariot and the river are mere words or names, and have no present real existence at all.”

“Then,” asked the sage, “tell me of what your real thought of the chariot and of the river must consist; of what is it composed; of what is it made up.” “Reverend sir,” replied the king, “I find that my real thought of the chariot, and of the river, is composed, constituted, and made up of my several ideas of their various parts, and of my idea of the combination, correlation and coordination of those parts; of those several parts existing, and being assembled, arranged, and put together in a certain fashion.” “Good,” said the sage, “you have now discovered for yourself the true nature of all things. Everything of which you can think is so composed, constituted and made up; so are the several parts, elements and factors ‘put together’ in a certain fashion, and acting in combination, coordination and correlation.”

Thus the ancient sage, employing the Socratic Method of delivering the mind of its thought by means of asking leading questions, taught to the king the lesson of the true nature of things, and thoughts of things. You may employ this method in the way of applying the general principle to anything and everything which is the subject or object of your actual experience, and which is the result of your processes of perception and conception. All Percepts and all Concepts are made up of “put together” parts, elements and factors of thought (as you have seen in the preceding section of this book); and, being so, they are each and all subject to analysis and resolution into such constituent elements.

In considering the subject of composition and analysis, however, you must not lose sight of the important part played in it by the respective forms of arrangement and correlation present in the “putting together” of the several elements, parts, or factors of a thing. For instance, there are many chemical elements, harmless in themselves, or harmless when combined in certain proportions, which are poisonous when combined in certain other proportions. The same is true concerning explosives; for instance, nitro-glycerine is composed of two harmless and non-explosive materials, which when combined in certain proportions produce the high-explosive. Formulas must include not only the constituent elements, but also the proportions in which these must be combined.

Carbon, in different forms, produces the diamond, charcoal, and other substances manifesting widely different appearances. From some seventy or eighty chemical elements, combined in different proportions, all the countless number of organic and inorganic material substances are made up and constituted. In considering the principle of Composition, the associated principles of Correlation, (i. e. mutual or reciprocal relation), and Coordination (i. e., common and harmonious action, movement or condition), must be also taken into consideration. The phenomena of Composition consist not only of the “putting together,” but also of the arrangement observed in the “putting together.”

The Law of Composition and Analysis manifests in the mental as well as in the physical field. In every field of Physics or Psychology it is found manifest. No exceptions have thus far been discovered. All apparent exceptions are ultimately found unquestionably coming under the rule.

Qualities, Properties and Attributes

Now for the definitions of the three terms, employed in that clause of our axiom following the symbol “(b),” viz., “qualities, properties and attributes.” A “Quality” is: “Anything that makes, or helps to make, anything such as it is; a distinguishing property, characteristic or attribute.” A “Property” is: “A peculiar quality of a thing; a distinctive attribute; an inherent and naturally essential characteristic of anything.” An “Attribute” is: “An inherent quality, essential property, or characteristic disposition.”

In the preceding section of this book, you have seen that in the act or process of Perception you recognize certain sensory reports (arising from contact with external objects) as being associated with those particular objects; and interpret them as representing certain qualities, properties or attributes inherent and abiding in those objects. In a Percept (as you have discovered) you regard the perceived elements as “representing qualities of the perceived object; these being incorporated into a group, giving the impression of a single and unitary whole, which is regarded as constituting the idea and meaning of that object.” Therefore, your Percept of a particular object is composed and made up of “put together” separate perceptions arising from separate sensations. Likewise, the object represented by your Percept is regarded as being composed and made up of the “put together” particular qualities, properties and attributes which are represented by the perceptive elements which constitute your completed Percept.

Illustration: When you perceive a particular Orange placed before you, you become conscious of a number of sensations arising by reason of the presence of the Orange, and of its contact with your sensory organism. These several sensations being recognized, interpreted, and associated with that Orange, are transformed into perceptive elements, and combined in your completed Percept of “that Orange.” Your Percept, then is composed and made up of several elements, each of which represents a particular quality, property or attribute of that Orange.

In the illustrative figure on the next page, we have (1) a circle representing your Percept of that particular Orange; and a number of smaller circles included in the limits of the larger one, each of which represents the perceptive element associated with some particular quality, property or attitude of the Orange, viz., (a) its form, (b) its weight, (c) its hardness or softness, (d) its color, (e) its fragrance, (f) its taste, (g) its size. Each of these respective perceptive element is called a “simple percept”; their fusion and union into the particular idea of “that Orange” constitutes a “complex percept”—technically known as “a Percept,” such as has been described to you.

 

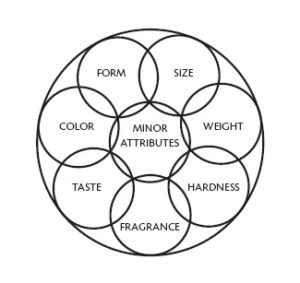
You should note here the important fact that you are able to distinguish between one object of thought and other such objects—between one perceived thing and other such things— solely by reason of your perception of the differences in the respective qualities, properties and attributes of the several objects or things. You distinguish and discriminate between objects and things solely by reason of your perception of their distinctive respective “characters.” The “character” of anything, i. e., “that peculiar quality, or the sum of qualities, by which a person or thing is distinguished from others,” is composed and made up of “characteristics.”

Characteristics

The term “Characteristics” means: “Distinguishing traits, qualities, attributes or properties.” In the category of Characteristics are found not only the qualities, properties and attributes which we have just considered, but also the parts, elements and factors and their arrangement, correlations and coordinations, which we considered a little further back in this section of this book. The Characteristics of a thing make it “just what it is”—that particular thing as distinguished from other particular things.

“External Characteristics.” In addition to the Characteristics (i. e., the qualities, properties and attributes; the parts, elements and factors) which we have considered in these pages, there are certain “quasi-characteristics” of things which some thinkers would include in the category of Characteristics or Attributes. These “quasi-characteristics” compose a class of relation-attributes, i. e., attributes denoting the relations known as “contiguity of time, space, and cause and effect” which the object bears to other things or objects. These relation-attributes are often called the “external characteristics” of the object or thing. Example: (a) the relation of Cause and Effect existing between two things; (b) the relation of nearness or distance in space between two things; (c) the relation of nearness or distance in time between two things.

The “quasi-characteristics,” or “external characteristics,” while properly “belonging to” an object or things, nevertheless are not true characteristics, such as the “internal characteristics” which we have previously described in the pages. The “internal characteristics” (i. e., the parts, elements and factors, the qualities, properties and attributes, of a thing) are essentially connected with the inner nature of that thing; while the “external characteristics” depend not upon the inner nature of the thing, but, instead, upon the external “conditions” under which the thing exists. By “Conditions” is meant: “The state, circumstances, or relative position in or under which anything exists.”

We shall consider the subject of “External Characteristics” in the following section of this book, which is devoted to the examination of “The Law of Logical Synthesis.” We believe this to be the more logical method of treating that particular subject, inasmuch as it is involved in Apperception, rather than in Perception.

The Law of Logical Synthesis

You are now invited to consider that important Law of Logical Reasoning known as the Law of Logical Synthesis.

This Law represents the universal experience of human thought, rationally applied and directed. The Law of Logical Synthesis is expressed in the second of the Seven Axioms of Logical Reasoning, which is as follows:

2. THE AXIOM OF LOGICAL SYNTHESIS: “Every thing belongs to a class of things possessing one or more common and essential characteristics; many things belong to several classes of different (though not opposing) character.”

The principle, law, and truth embodied in this axiom is employed in all logical thinking. It is regarded as a self-evident truth, properly to be taken for granted; it is assumed in all logical thought, and is implied in all true reasoning. The following consideration is not intended to be offered as proof of its truth; but is designed merely to elucidate and make clearer the manifestation of this principle in the world of thought and things.

By “Logical Synthesis” is meant: “The act of synthesizing, combining, putting together, or arranging systematically into classes or groups, two or more individual or particular things possessing common essential characteristics.” By “Class” is meant: “A group of individual or particular things possessing common essential characteristics.”

The principle of Classification, as employed in Logical Reasoning, is applied under two general methods, viz., (1) the method of Practical Classification, and (2) the method of Logical Synthesis. Practical Classification consists of placing particular things (represented by their appropriate Percepts) into loosely constructed classes depending upon the general resemblance discovered to exist between the respective characteristics of such things; this form of Classification is employed merely for convenience of thought and expression. Logical Synthesis consists of the processes whereby Reason unites into a General Idea or Concept the several elements of a number of particular Percepts bearing a very close resemblance to each other in the matter of their essential characteristics. This form of Classification or Synthesis has for its purpose the creation of an intelligent idea of a general class, genus, or species of things; such created ideas afterward to be used as material for the higher processes of Logical Reasoning or Logical Inference. We now ask you to consider in further detail each of these two general methods of Classification.

Practical Classification

By reference to your own experience, you will find that you are in the habit of grouping your ideas of things into certain loosely-knitted classes; you think of them as “all of a kind,” for the purpose of convenience, yet you do not make the subdivisions into genera, species, families, etc. Your ordinary classification of this kind, you will find, arises from your perception of certain general kinds, forms, or classes of relationship existing between the particular things in question.

Examples of this kind of relation between particular things are found in cases of: (1) the relations of existence in the same place; (2) the relation of existence in the same period of time; (3) the relation of cause and effect, as for instance, thunder and lightning; (4) personal relations, as, for instance, parent and child, husband and wife, brother and sister, etc., (5) mass relations, as, for instance, members of the same religious denomination, the same political party, the same base-ball team, the same legislature, the same club, etc., (6) utilitarian relations, as, for instance, coal and fire, oil and light, steam and motive-power, etc., (7) relations of common purpose or use, as, for instance, coal, wood, and oil (considered as heat-producers), or candles, oil, and electric-light (considered as light-producers); (8) relations of resemblance of prominent characteristics, as, for instance, all black things, all sweet things, all solid things, all poisonous things, all explosive things; (9) the special relations of whole and parts, as, for instance, the automobile and its numerous parts, fixtures and attachments. This list of possible Practical Classification might be extended almost indefinitely; but the above mentioned more important classes will serve to illustrate the principle employed and observed in all such classification.

You will find it of great importance to cultivate this form of Classification. By tying your notions of things into separate bundles—by placing them in the appropriate pigeon-holes of memory—by “cross indexing” them, as it were—you will be able to perform your work of Practical Thinking and Efficient Thought with a minimum expenditure of time and effort, and with a maximum of desirable results.

Put things into Classes in your mind—but be careful that each thing properly belongs in that class, else you may experience trouble when you have need to refer to that class of things. You cannot well classify things properly unless you have previously acquired clear and correct Percepts or Concepts of them. The man who has the materials of thought well classified and systematically arranged, will be able to “think out” the desired answer long before the man not so prepared is able to do it— indeed, the latter person may not be able to do it at all. System in the Classification of ideas, information and knowledge will give one an immense advantage over others who follow the “higgledy-piggledy” method—or lack of method.

Professor Halleck well says: “Whenever a person is comparing a fact in order to put it in the same class with other specimens, he is Thinking. Comparison is an absolutely essential factor of Thought, and Classification demands comparison. The man who has not properly classified the myriad individual objects with which he has to deal, must advance like a cripple. He, only, can travel with seven-leagued boots who has thought out the relations existing between these stray individuals and put them into their proper classes. In a minute, a business man may put his hand on any one of ten thousand letters, if they are properly classified. In the same way, the student of any science can, if he studies his subject aright, have all of his knowledge of any subject classified and speedily available for use.”

You will be able to put the same thing into very many classes, under the method of Practical Classification. The more classes, the better; for each class-relation gives you another handle with which to grasp the thought of that thing when you need it; each is another “cross index” by means of which you may find it when it is required.

Some psychologists indicate the process of Practical Classification by the name or term, “Apperception,” so as to distinguish it from the Classification of Logical Synthesis known in Logic as Conception. The important mental process known as Apperception is overlooked in most works dealing with the subject of Formal Logic; indeed this particular subject belongs rather to the field of Practical Logic. Professor Gordy says: “Apperception is the most fundamental form of mental activity. It is that combining activity of the mind that brings order and harmony of related facts into the consciousness of relations.” In the processes of Constructive Imagination, the factor of Apperception, or “the knowledge of practical relations,” is a very important element.

The Law of Logical Synthesis Practical Logic is largely concerned with the discovery of the practical relations between things; and the proper classifications of such relations. Unrelated knowledge is only half-knowledge. Be keen in your search for relations; and be careful in your classification of them after they are discovered. Men advance by reason of their discovery of new relations in things; and by properly classifying and indexing these in their minds. Halleck well says: “Whenever one learns a new thing, apparently unrelated to any other part of his knowledge, he should make haste to form connections. In doing this, he will think”

This, then, is what the method of Practical Classification means; as for the method of Logical Synthesis, or Generalization—”that is another story.” You have doubtless noted that under the method of Practical Classification the arrangement into classes is made according to the “quasi-attributes,” or the “external characteristics” of the different things, rather than according to the true qualities, properties, and attributes—the “internal characteristics” of the different objects. In Logical Synthesis, or Generalization, the division and classification proceed according to strict logical requirements; in it only the true qualities, properties and attributes are taken into consideration—only the “internal characteristics” are employed in the process of Logical Classification.

Logical Synthesis, or Generalization

Logical Synthesis, or Generalization is: “The act or process of bringing two or more particular Percepts, agreeing in some important point or points of character, into a common or general class, under a common or general head, name or term; or to bring a particular fact, or series of facts, into a wider circle of similar facts, to which an appropriate term has been affixed. The general idea, class or conception thus produced is known as a Concept. The Concept, so produced, is the general idea or notion; or the idea or notion of a general class of things, which is composed, constituted and made up of a number of particular ideas of particular individual things possessing class-characteristics in common. The term applied to the Concept becomes the class name.”

In Logical Synthesis, or Generalization, the term “class” does not (as in Practical Classification) mean merely a crowd, collection, aggregation or assembled number of individuals not necessarily possessing essential “internal characteristics”; instead, it here clearly means an indefinite number of individual things (perhaps far apart in time or space) which possess certain essential “internal characteristics” in common, and which are practically identical and “alike” in these essential respects.

In Logical Synthesis, or Generalization, many individual things are carefully compared for “resemblances” and agreement; their respective non-essential “differences” and disagreements bein g laid asi de in the general classifi cation . That is to say, if the several things agree in the major characteristics, then their disagreements in their minor characteristics are overlooked in the general classification. These minor disagreements, however, may later form the basis for the formation of sub-classes, etc. Agreements are the basis of Synthesis; Disagreements are the basis of Analysis.

In this way, all Concepts of Classes, Orders, Families, Species, and Genera arise. Let us take the general Concept of “Bird” as an illustration. The conceptual term, “Bird” is defined as: “Any and every feathered, winged, warm-blooded, egg-laying, biped vertebrate; great or small, young or old.”

Here, then, are the essential common parts, elements and factors, qualities, properties and attributes, which each and every bird, and all birds (in normal condition) must possess in order to constitute them true Birds, viz., (1) A vertebra; (2) two legs; (3) wings; (4) warm-blood; (5) feathers; (6) egg-laying functions in the female; (7) all in combination in the same animal, at the same time. Bats and butterflies are not birds, though they have wings; flying-fish and flying-squirrels are not  birds, though they fly; reptiles are not birds, though some of them lay eggs; and so on: all the essential characteristics must be present in the same animal, at the same time; the creatures just mentioned, while possessing some of these characteristics, lack others, and so cannot be Birds.

The Concept of “Birds” may be synthesized into the greater Concept of Vertebrates; and this, in turn, into the still greater Concept of Animals; and this, again, into the still more general Concept of Natural Objects. Likewise, the Concept of “Birds” may be analyzed and separated into its various subclasses, families, species, sub-species, varieties, etc. As we have already said, “Synthesis proceeds according to resemblances; Analysis proceeds according to differences.”

Note: It must not be overlooked that while the stricter and more precise forms of Logical Classification deal with Concepts of classes composed of many individuals having only a few common characteristics, yet there are certain forms employed in Logical Reasoning in which a certain variation of this particular principle is manifested. These forms are as follows:

A. Class Concepts in which many objects or individuals possess practically only one common essential characteristic; and (2) Class Concepts in which are included merely one individual or object having one or more special characteristics. Examples of each are given in the following two paragraphs.

B. The Class Concept may include many individuals having practically but one common essential characteristic; as, for instance, Class Concepts of “white things,” “colored things,” “beautiful things,” “live things,” “dead things,” in fact, any kind of things having but one essential quality necessary to admit them to the class. Any quality or condition may serve as the basis for such classification, and as the one essential quality or element of such Concept. Thus when we say: “This thing is sweet,” we place it in the class of “sweet things,” the one essential attribute of such class being “sweetness.” The Class Concept may include only one individual or object having one or more special qualities, or conditions. For example: The Eiffel Tower, the Capitol at Washington, the Washington Monument, the Rosetta Stone, Niagara Falls, Napoleon Bonaparte, are each “in a class by itself,” and each has some special characteristic distinguishing it from all other things. Here the individual or object constitutes the “whole thing” of its special class.

These two special forms of Class Concepts are, of course, capable of being synthesized into greater Class Concepts; but only the first-mentioned may be analyzed into sub-classes; the latter defies analysis of this kind, for its consists of only one individual.

In forming Concepts by Logical Synthesis, or Generalization, care must be taken to discriminate between (1) the “essential characteristics” of the various individual things you wish to combine into a general class; and (2) the “non-essential characteristics” possessed by some (but not all) of the particular things. An “essential characteristic” is “a characteristic which is common to the whole class; one which is necessary to entitle the individual to admission to the class.” A “non-essential characteristic” is “a characteristic which a member of a class may, or may not have, which is not necessary to admit him to the class, but which does not debar him from it.”

The true “essential characteristics” of the “Bird” Concept are those previously noted, viz., vertebra, two legs, wings, warm-blood, feathers, egg-laying, in combination in the same individual. The “non-essential attributes” possessed by the individual members of the class, are, for example: differences in coloring, in general or special conformation, size, food-habits, nest-building-habits, configuration of beak, bill, feet, wings, tail, body, etc. Such widely varying creatures as owls, sparrows, eagles, condors, vultures, wrens, humming birds, cranes, storks, crows, ostriches, parrots, wood-peckers, etc., all have the “essential characteristics” denoting Bird-ness; yet each has many “non-essential characteristics” which have “nothing to do with the case” of their Bird-ness.

The Concept is a mental symbol; yet it cannot be pictured as a mental image. The mind is able to grasp the conceptual symbol of “Bird,” yet it cannot picture the Concept “Bird”; it cannot visualize it! Think over this for a moment, and you will see just why this is so. You may visualize or picture a bird; but you cannot do this with the abstract conceptual idea of “Bird” (i. e., all birds). This, because of the ever-present “non-essential characteristics” found in each and every bird, in different form and kind—each bird having some of them, but no bird having all of them; each of them is present in some birds, but none of them is present in all birds.

A picture of the Concept “Bird” (i. e., All-Birds) would have to portray a creature having, at the same time and place, the long legs of the crane or stork, and the short legs of the wren or sparrow; the long bill of the hummingbird, the snipe, etc., the short bill of the sparrow or wren, and the beak of the eagle; the claws of the hawk, the feet of the chicken, and the web-feet of the duck; the neck of the swan, of the crane, of the wren, of the sparrow, and of the duck; not to speak of the almost infinite variation of color, size, relative proportions of the several parts of the body, etc. An attempt—even a feeble attempt—to produce such a picture would result in a production equalling the vision of the sufferer from delirium tremens, or the creation of some of the “post-futurist” schools of art. So, you see, the Concept can exist merely as a mental symbol; never as a mental picture. Like the mathematical symbol, it exists merely for the purposes of work. Without such symbols, moreover, Logical Reasoning would be impossible.

Rules of Logical Synthesis, or Generalization

The following are the technical rules employed in the formation of Concepts by Logical Synthesis, or Generalization.

1. Discover the Essential Characteristics. First discover the essential characteristics necessary to admit the particular individual things into the general class, entitling them to the class-term, and making the ideas of them proper elements of the Concept. This is done by comparing the individuals regarded by you as promising candidates for admission to the class. This comparison will reveal (a) characteristics possessed by only some of the individuals. These cannot be cancelled; therefore, they are perceived to be essential characteristics of that class of things, and, consequently, are the essential elements of the Concept representing that class.
2. Admit Only the Essential Characteristics. Admit to the Concept only the essential characteristics which have been discovered in the class. Rule out the cancelled non-essentials. The essential characteristics of the class constitute the essential elements of the Concept. Nothing but such essential elements belong to the Concept. Nothing that does not belong to the Concept must be included in it.
3. Include All Qualified Individuals. Include in the Concept each, every, and all individual Percepts, or lesser Concepts, which possess all the essential elements, i. e., all the essential characteristics of the class; but exclude all individual Percepts or lesser Concepts which have not all such essential elements. The Concept must include all that belongs to it; but nothing that does not belong to it.
4. Synthesize in Logical The synthesis of the individuals into classes, and of these into higher classes, should proceed according to logical sequence, i. e., (a) from lower to higher, (b) from simple to complex, (e) without omission of a logical intermediate stage—without a “logical break.” For instance: It is illogical to synthesize “horses, trout, and swallows” directly into the great class of “Animals”; here, the logical method and sequence requires the recognition of the respective intermediate classes known as “mammals,” “fishes,” and “birds,” before the great class of “Animals” is reached.
5. Synthesize in Uniform Order. The process of synthesis should proceed in uniform order, and according to the principle of classification adopted in beginning it. For instance: It is logical to classify individual men, either (a) according to race, as, for instance, into the sub-classes known as Caucasians, Mongolians, American Indians, etc.; or (b) according to religion, as, for instance, into the sub-classes known as Christians, Buddhists, Atheists, etc. But it is illogical to confuse and confound these two respective divisions of classification.

We may logically group men into branches of a great religion, and these into divisions, and these into the whole great religious class itself. Likewise, we may logically group men into sub-races, these into minor races, these into major races, and these into the whole family of Mankind. But it is illogical to classify men as follows: Caucasians, Buddhists, Mongolians, Christians, American Indians, Atheists, etc. This, because such classification is contrary to Nature, lacks rational order, and is confusing and misleading; this being so, it tends to fallacious reasoning when its faulty Concepts are employed in Induction or Deduction.

You will see this more clearly if you stop to consider that a Caucasian may be either a Christian, an Atheist, or a Buddhist, but be cannot be either Caucasian or an American Indian—he must remain a Caucasian. Likewise a Mongolian may be either a Buddhist, a Christian, or an Atheist—but he cannot be a Caucasian. The validity of this rule arises from the fact that it agrees with the foregoing four other rules; when it is violated, one or more of the other four rules (usually, all of them) are likewise violated.

Note: We would call your attention here to this important principle involved in all Concepts or Logical Classifications: “The more general the class the fewer are its essential elements or characteristics and the larger the number of individuals included in it. Likewise, the less general the class, the more numerous are its essential elements or characteristics, and the fewer are the number of individuals included in it.” Example: Consider the following Concepts in the light of the above statement, viz., “Bird”; “Finch”; “Sparrow” (a particular member of the Finch family); “Chippy” (a particular member of the Sparrow family); “That particular Chippy” (a particular individual of the Chippy family). Here you pass from the consideration of “All Birds,” comprising countless individuals with but very few essential characteristics, by gradual stages down to the consideration of but one bird with a multitude of essential characteristics (each individual, in a sense, is “in a class by itself” inasmuch as no two individuals are precisely alike).

The Law of Logical Judgment

You are now invited to consider that important Law of Logical Reasoning known as the Law of Logical Judgment. This Law represents the universal experience of human thought rationally applied and directed. The Law of Logical Judgment is expressed in the third of the Seven Axioms of Logical Reasoning, which is as follows:

3. THE AXIOM OF LOGICAL JUDGMENT: “All Logical Judgment is based upon these three fundamental Laws of Thought, viz., (1) A thing is always just what it is, and nothing else; at a given time and place, no matter what name or term may be employed to indicate, designate or represent it; (2) A thing cannot both be and yet not be just what it is affirmed to be, at the same time and place; (3) A thing must either be, or not be, that which it is affirmed to be, at a given time and place—there is no third alternative.”

This axiom embodies the essential principles of the ancient “Three Laws of Thought” which were first stated nearly two thousand years ago by the old Greek philosophers. In their original form they were as follows: “Whatever is, is; No thing can both be and not be; Every thing must either be or not be.” These laws are known, technically, as “The Law of Identity,” “The Law of Contradiction,” and “The Law of Excluded Middle,” respectively.

Jevons has said of these laws: “Students are seldom able to see at first their full meaning and importance. All arguments may be explained when these self-evident laws are granted. It is not too much to say that the whole of Logic will be plain to those who will constantly use these laws as their key.” The three divisions of the Axiom of Logical Judgment (embodying these three Laws of Thought) will be considered in detail as we proceed with our instruction concerning the Law of Logical Judgment in this section of this book.

Judgment is: “That mental process involving comparison and discrimination (i. e., discernment of resemblances and differences in the qualities of respective Percepts or Concepts), where the mind forms opinions and decisions concerning the nature of the things under consideration.”

Judgment is that power of the Reason whereby it perceives the agreement or disagreement between two objects of thought. Reason, in the process of Judgment, compares and decides. It is manifest in every act of reasoning thought. It manifests when you form your Percepts, when you create your Concepts, when you state your Propositions, when you make your Inferences. The mind cannot reason without employing Judgments; to reason is to judge, to judge is to reason. Reasoning is a continuous process, and Judgment is always involved in it. Reasoning is the golden thread upon which are strung the pearls of successive Judgments. Logical Reasoning is “one Logical Judgment after another.”

Let us now consider in detail the three elements involved in the Axiom of Logical Judgment which expresses the Law of Logical Judgment.

The Law of Identity. The first element of the Law of Logical Judgment is that originally known as “The Law of Identity,” which in our axiom is as follows: “A thing is always just what it is, and nothing else, at a given time and place, no matter what name or term may be employed to indicate, designate, or represent it.”

The first part of this statement, i. e., that “A thing is always just what it is, and nothing else, at a given time and place,” is so thoroughly self-evident that it requires no argument to substantiate it; in fact, the student first having it presented to his attention, is often inclined to regard the statement as a waste of words—its truth is so clearly evident. Its importance is realized only when one encounters fallacious reasoning in which the rule is violated.

This principle, like the bee or wasp, “has its sting in its tail”; the rest of it is comparatively harmless. The sting-containing tail is as follows: “no matter what name or term may be employed to indicate, designate or represent it.” Let us carefully examine this “sting” which wounds so many who trifle with it.

Let us begin by reminding you that, “Most arguments are really disputes over terms, rather than about facts.” Again, that: “Rational argument or thought is impossible without a preceding agreement upon the meaning of the principal terms employed.” Once more: “The essential point of issue of an argument once properly stated and clearly defined, the argument is then at least partly completed—sometimes fully completed.” The first rule of Reasoning based upon Practical Logic is: “First, define your terms.” Careful observation will show you that most disagreements and arguments are really “disputes over words.”

So, you see, in order to apply the principle that “‘A thing is always just what it is, and ‘nothing else,” you must first find out the “just what it is” of the thing under consideration— the subject of reasoning, thought, argument, dispute. This is accomplished by ascertaining and formulating the logical definition of the term most fitly indicating it. The following suggestions will prove useful to you in this direction.

Logical Definition. First, impress upon your mind the following statement: “My full idea of just what a thing is, is expressed in a full, exact, and complete definition of the logical term indicating it. A dozen different names and terms may be applied to that thing in common speech, discussion or argument; but its essential logical meaning is not altered in the least by reason of changes of names or terms—the thing remains ‘just what it is’ in spite of the changed names or terms. Before I attach a name or term to a thing, in logical thought, reasoning or argument, I must be certain that such name or term fitly, completely and logically designates that thing. I must also remember that a name or term indicating more than one thing is practically several names or terms.”

The following statement of the leading requisites of a Logical Definition will serve to indicate the character of the latter: (1) The definition should state all the essential characteristics of the thing; (2) Non-essential characteristics should not be stated in the definition; (3) Names or terms indicating the thing should not be included in the definition—it is illogical to define a thing by itself, or in its own terms; (4) The definition should be stated in affirmative terms, negative terms being avoided so far as is possible; (5) The definition should be stated in plain, clear terms—all obscure, ambiguous, or equivocal terms (terms capable of several possible meanings, or conveying only vague, hazy and confused meanings), as well as all figurative language, being avoided. You will discover that but very few such logical definitions are employed in ordinary, popular argument, debate, dispute, or reasoning thought—hence, the great number of fallacies apparent in such.

Socrates, the famous Greek philosopher, held that a logical definition contained in itself the answer to most of the questions and problems vexing the mind of man. Accordingly, he formulated the now famous “Socratic Method” which consisted of having his pupils answer, in the form of logical definitions, his questions concerning the essential and fundamental nature and character of the things under discussion. Thus, he brought them down to first principles, or, in the words of the current popular phrase, “down to brass tacks.” He made them solve their own problems in this way. He “delivered” them of their essential ideas—his method was obstetrical. Socrates held that most questions and disputes arose over “the meaning of words and terms”: he was a wise man!

The “Socratic Method,” reduced to its simplest elements, may be applied by you in reaching your logical definition in which is to be stated “just what this thing is,” in the following three forms:

• Ask yourself the questions: “What are the essential parts, elements and factors involved in this thing? What are its essential qualities, properties and attributes? What are its causes? What are its effects? How does it act? What work does it perform? What does it do? Of what greater thing is it a part; into what class, or classes, of things does it fit?
• Ask yourself the following questions: “What? When? Where? How? Why? What follows?”
• Ask yourselves the following questions: “What is it? How do I know it? What of it?”

These three simple forms of applying the “Socratic Method” will serve to “deliver” your mind of much essential information concerning the thing in question; this will aid you in formulating and passing upon the logical definition of that thing.

It is difficult to leave the subject of Socrates in this consideration of the Law of Identity; for that old philosopher made this law his cardinal principle; his teaching was based largely upon its truth and the means whereby it might be applied in practical reasoning. Socrates had become disgusted with the notorious practices of the Sophists, particularly with their habit of quibbling about terms and the names of things. He objected especially to their employment of forms of argument which amounted to but little if anything more than “a play upon words”—a species of “punning” in extreme cases. So, he emphasized the Law of Identity, and asserted that “a thing is always itself, no matter what name may be attached to it”; and that it is one’s business to find out “just what” the thing is. To him “White” was none the less white if the name “Black” was applied to it. He insisted that “calling a thing so, does not make it so.” He was opposed to the bad habit of “calling things wrong names.”

Socrates cautioned his pupils always to be on guard against arguments, or processes of quasi-reasoning, which are really but disputes about terms and names, and in which the “suchness,” the “whichness,” and the “thingness” of particular things are either carelessly or else deliberately ignored. His favorite aphorism was: “Reason about Things, not about terms or words.”

A noted modern logician has expressed the spirit of the Socratic thought in the following words: “Whatever is actually true of one term is also actually true of any term which is stated to be the same in essential meaning as the first term. Terms may be substituted, one for the other, provided that it is agreed that they refer to exactly the same things.” Even the symbol “X” may be substituted for the class-term “Bird,” if it be agreed that by “X” is meant “feathered, winged, warm-blooded, egg-laying, biped vertebrate.” Do you get the idea? It is this: “It is the meaning of the term, not the form, letters or sound, that counts.”

Before leaving the subject of the Law of Identity, let us give you a few concrete examples of its value—a few real proofs of its virtue. The study of Fallacy arising from the violation of a Law of Logic will go further toward proving the value and virtue of that law than will much greater study of its technical principles and meaning. The results of the violation of any valid law will bring to one the most convincing proofs of its validity; this is true in every branch or field of human thought or action.

Illustrations of the Law of Identity.

The following examples serve to illustrate the general principles of the application of the Law of Identity:

Professor William James, in one of his essays, tells of a hunter who saw a squirrel clinging to the trunk of a tree. The hunter Judgment walked slowly around the tree to which the squirrel was clinging; the squirrel, at the same time, moved around the trunk of the tree so that its back was never presented to the hunter. Query: Did the hunter “walk around” the squirrel, or did he fail to do so? According to the laws of Logical Reasoning, he must either have “‘walked around” the squirrel, or not have done so; he could not both have done so and yet not have done so—it must be one thing or the other, but which? This “trick-question” has perplexed many keen, practical minds at first; to many it has seemed like a problem “in Einstein.” But it really is “sophistical” in the form stated—the form so strenuously objected to by old Socrates; when the Law of Identity is applied to it, the difficulty vanishes.

The gist of the question depends upon another question, viz., “just what is meant by ‘walking around’ the squirrel?” If by “walking around the squirrel” is meant that “the man proceeded so as to face in turn both the back and the front of the squirrel,” then the answer must be that he did not do so. If, on the contrary, by “walking around the squirrel” is meant that “the man proceeded so as to move completely around the place where the squirrel was situated, i. e., the trunk of the tree,” then the answer must be that he did so. Without an agreement upon “just what” is meant by “walking around”—the logical meaning of the term—there can be no logical judgment; but this agreement once reached, this meaning once established, there can be but one logical judgment—and that a very easy one at which to arrive. The Law of Identity governs this case, when its principles are logically applied; and in it you have an example of the virtue of the rules: “Define your terms,” and “Reason about Things, not about words.”

Another example: A Whale is popularly known as a fish; it looks like a fish, it swims like a fish, it lives in water like a fish. Then, is or is it not a fish? Popular opinion holds that it is a fish, because of the characteristics above noted. Naturalists hold that it is not a fish, because it is a mammal, has lungs, is warm-blooded, and suckles its young at its breast and gives it milk, just as does any other mammal. Which is right? The disputants might argue indefinitely unless there was some agreement upon the meaning of the term “Fish”; some logical definition of it. Reference to capable and competent authorities show that: “A fish is cold-blooded, has gills, and does not suckle its young, having no teats or mammary glands to do so.” This scientific meaning of the term “Fish” being ascertained and accepted, this answer immediately follows: “The Whale is not a fish, though it looks like one and lives and swims in the water like one.” On the contrary, the same reasoning shows that the Whale, having all the essential qualities of a “mammal,” is and must be a mammal.

Another example: A person asserts that the water in the bath-tub is “hot,” another says that it is merely “warm,” a third holds that it is “tepid,” a fourth believes that it is “cool.” How is the dispute to be settled? Each reports the degree of “heat sensation,” or rather the “heat perception,” experienced by himself. Yet the temperature of that water remains certain, definite, fixed, at least for the moment. Lacking a standard of meaning governing the use of these several terms, there can be no agreement. The thermometer gives the certain, definite, fixed temperature; but it does not report whether such be “hot,” “warm,” “tepid,” or “cool”—neither does the dictionary. Let us suppose that the disputants agree to accept the definition given by certain authorities on bathing. These authorities report that: “Water is hot when its temperature is above 98 deg. Fahr.; that it is warm from 85 to 98 deg. Fahr.; that it is tepid from 75 to 85 deg. Fahr.; that it is ice cold at 32 deg. Fahr. This, or any similar standard, once accepted or adopted, the Judgment becomes certain—the thermometer gives the true answer.

Another example: A particularly dangerous form of Fallacy claiming the protection of the Laws of Thought is that which arises from the assumption of some relative, comparative or personal opinion by which the actions of persons or the character of things are measured. The Fallacy consists in assuming that such relative, comparative or personal opinion represents an actual, fixed, certain standard, instead of being one dependent entirely upon the personal views, opinions, training or prejudice of the individual employing it. For instance, it is often argued that such a person is “noble,” “courageous,” “virtuous,” “vicious,” “selfish,” “unbusinesslike,” etc., etc., etc.

Such reasoning or arguments are always more or less futile and inconclusive, because no fixed standard is agreed upon or accepted—no fixed measure of value agreed upon or accepted by the disputants. If some such fixed standard (as, for instance; one representing the best opinion of the time and place) is agreed upon and accepted, then the Judgment is speedily reached. In absence of such, the reasoning or argument travels round in a circle, ever moving but never reaching a conclusion. The rule in such cases is this: “Define your terms; obtain an agreement upon the standard of measurement or value; and THEN reason logically from such.” One is even justified in inquiring of others, or of himself, “good for what,” when the argument or reasoning is concerned with the question or whether or not a certain thing or action is “good.”

Other examples illustrating the need of clearness of definition of terms are found in the later section of this book, entitled “The Law of Deduction,” under the head “The Terms Must Be Unequivocal and Not Ambiguous.” That portion of our instruction should be studied and considered in connection with the present statements—and vice-versa—for they are both concerned with the same principle of Judgment.

The Law of Contradiction. The second element of the Law of Logical Judgment is that originally known as “The Law of Contradiction,” which in our axiom is stated as follows: “A thing cannot both be and not be just what it is affirmed to be, at the same time and place.” We shall consider this logical principle in connection with “The Law of Excluded Middle,” inasmuch as the same essential principle is involved in each, and in both; the two laws being complementary one to the other.

The Law of Excluded Middle.

The third element of the Law of Logical Judgment is that originally known as “The Law of Excluded Middle,” which in our axiom is stated as follows: “A thing must either be, or not be, that which it is affirmed to be, at a given time and place.”

In the case of these two respective laws, as in the case of the one which we have just considered, the “sting” is found in the tail. In these cases, the “sting” consists of the clause contained in the statement of each, i. e., “at the same time and place,” or “at a given time and place.” When this point of “time and place,” and that of “definition of terms,” are fully understood, the application of these two principles becomes easy. The words, “at the same time and place,” or “at a given time and place,” give additional definiteness to the proposition, and serve to bring into a clear relief its essential meaning.

The valid application of these two principles is illustrated by the following familiar examples: “You are either just where you are, or not just where you are, at the time you are reading these words; you must either be there, or not be there—you cannot both be and yet not be there, and there is no third alternative in which the two extremes are harmonized, or in which neither is the truth. This requires no argument—it is self-evident. Again: A dog must either be an animal, or else not be an animal (at a given time and place); it cannot both be and yet not be such— and there is no third alternative. This is self-evident. Again: A particular rose, at a given time and place, must either be “red,” or else “not red”; it cannot both be and yet not be “red”—and there is no third alternative. Again: A whale must either be or not be a fish; it cannot both be and yet not be—and there is no third alternative.

Such cases might be multiplied indefinitely. The principle involved is self-evident; it is “as plain as the nose on your face.” It is only when we consider the unwarranted and fallacious attempts to employ the principle that its importance is made clear. Let us now consider a few examples of this fallacious application.

• The Element of TiME and Place. The time-element and space-element must be taken into consideration in the logical application of the Laws of Contradiction and Excluded Middle, respectively. While it is impossible for a thing both to be and yet not be so-and-so or such-and-such, at a given time and place, or at the same time and place; and while it is impossible for a thing to avoid either being or else not being that under these conditions; yet it is quite possible for a thing to be such-and-such at one time and place, and not to be such-and-and such at another time and place. Example: A piece of iron may be red-hot at one time, and not red-hot at another time. Likewise, a piece of iron may be red-hot at one end (i. e., one place) and not red-hot at the other end (i. e., another place). But at the same time and place it must be either red-hot or not so; it cannot be both, and it must be either.

Again: A man may be angry at one time and place, and not angry at another time and place; but at the same time and place he must be either one thing or the other—he cannot be both. Again: A piece of cloth may be red in one place (one part) and blue at another at the same time; or it may be red today, and be dyed purple tomorrow: but at the same time and place it must either be red or not red—it cannot be both. Query: A man has cold feet, and a hot head; is he “hot” or is he “cold”? If so; why? Are the principles of Logical Judgment overcome, or their laws violated, in such a case? In this connection, you are asked to note that even in such cases as those above cited, the Law of Identity governs: the thing or man, at any given time and place, is always “just what it is” at that time and place— notwithstanding “just what” that “just what” may be found to be.

• The Element of RELATiVE The distinction between absolute terms and relative terms, to which we have alluded in the preceding pages, also plays an important part in the application of these two laws or principles. Relative, comparative or personal terms must not be employed as absolute, fixed, certain, definite terms in such application. We have already given you a typically illustrative example in the case of the water in the bathtub. Differences of opinion concerning the “warmness” or “coolness” or “just rightness” of the temperature of a room furnish another example. Here, the absolute, certain, fixed, definite “just what” the temperature is consists of the report of the thermometer that “it is so many degrees, Fahrenheit.” Whether it is “cool,” “warm,” or “just right,” is a matter of individual feeling, unless a fixed standard be accepted or adopted, by means of which these terms acquire a definite meaning.

Here is a variation, illustrating the same principle: A man stands before three different basins filled with water. The right-hand basin contains water heated to 120 degrees Fahrenheit; the left-hand basin, water cooled to 35 degrees, Fahrenheit; the middle basin, water heated to 75 degrees, Fahrenheit. The man places one hand in the “cold” basin; his other hand in the “hot” one; and holds them there until they distinctly feel the respective kinds of temperature. Then, he withdraws both hands, and suddenly plunges them into the water in the middle basin—which is heated to 75 degrees, Fahrenheit. This causes his “hot water hand” to feel cold; and his “cold water hand” to feel warm; by reason of the contrast.

Query: Is the water of the middle basin “cold” or “not cold?” One hand says one thing: the other hand, another. How and why do the Laws of Logical Judgment apply in this case. The answer is: The only certain fact is that the water in the middle basin is “of a temperature of 75 degrees Fahrenheit.” Only this and nothing more; the rest is a matter of interpretation of sensation according to the existing conditions. If water of 75 degrees, Fahrenheit, be regarded (as it is) by authorities as “tepid” or “lukewarm,” then the water must be regarded as so, notwithstanding the conflicting reports of sensation made by the respective hands.

(Note: If two thermometers disagree in their reports, get a standard one, and abide by its decision.)

We advise you to fix the words “lukewarm water” in your memory, associating them with the above typical example. By doing so you will have at hand a convenient and useful reminder not to commit the Fallacy of confusing relative terms with absolute ones—personal feelings with fixed standards— permanent values with temporary ones. When you hear men arguing about their states of feeling, or their “notions” which they mistake for fixed, absolute standards and values, remember the story of “the hot hand and the cold hand, and the tepid water in between.” We shall not, however, here press the additional point that “the truth is found between the two extremes”—although this, too, is a fact of general experience, it is, nevertheless, “another story” and must be told elsewhere.

• The Element of False Another perplexing and frequently experienced obstacle to the proper application of the laws and principles now under consideration, is that which arises from a confusion concerning the logical “opposite” of a certain attribute, property or quality of an object.

Thus, many persons think that the true opposite of “white” is “black”; upon this basis one applying the rules of the respective Laws of Contradiction and Excluded Middle would be compelled to reason as follows: “This thing before me must be either white or else black, for it cannot be both, and there is no third alternative.” This reasoning is, of course, fallacious, for the thing in question might be neither white nor black; it might be green, or yellow, or blue, or orange, or purple, or any other color—it might even be colorless—without our rules being violated. The explanation lies in the fact that “black” is not the logical “opposite” of “white”: the true logical “opposite” of “white” being “not-white.” All other colors are in the “not-white” class; and it may be stated with logical certainty that “everything that exists must be either ‘white’ or else ‘not-white’—it cannot be both, and there is nothing else for it to be but one or the other of these.”

The same state of affairs is found in the respective cases of the apparent “opposites” known as “hot and cold,” “sharp and dull,”—and of all other cases in which the contrasting terms represent conditions manifested by the two extreme poles of a general class of things or characteristics; there being many degrees of difference between these two extreme poles. The same rule applies in cases like “Republican and Democrat.” “Catholic and Protestant,” etc. A man may be neither a Republican nor a Democrat; neither a Catholic nor a Protestant; for there is always a “third alternative,” or “a something else to be,” in such cases. The proper grouping of the “opposites” in these cases is as follows: “Republican or non-Republican; Democrat or non-Democrat; Catholic or non-Catholic; Protestant or non-Protestant.” Thus, each and every man that lives, no matter what may be his politics or religion—even if he be without political or religious affiliations—must be either a Republican or a non-Republican; a Democrat or a non-Democrat; a Catholic or a non-Catholic; or, for that matter, either the King of England or “not the King of England.” The little prefixes “not” or “non” indicate the true logical “opposite” to anything whatsoever, when attached to the name or term designating that thing.

The combined Laws of Contradiction and Excluded Middle, rightly understood and logically applied, are found to possess the absolute character of arithmetical or geometrical laws and principles. No true exceptions to these laws ever have been discovered; every apparent exception, when analyzed and explained, becomes an additional verification. The human mind is compelled to think according to these laws, when it reasons logically.

The Law of Logical Analogy

You are now invited to consider that important Law of Logical Reasoning known as the Law of Logical Analogy. This Law represents the universal experience of human thought rationally applied and directed. The Law of Logical Analogy is expressed in the fourth of the Seven Axioms of Logical Reasoning, which is as follows:

1. THE AXIOM OF LOGICAL ANALOGY: “A few things which are alike in many respects are probably (though not certainly) alike in some other respects.”

The principle of reasoning is the one most frequently employed by the average person; many, indeed, but seldom use any other form. Rightly understood, and employed within proper limits, it constitutes an important rule of rational thought; but the possibilities of the careless and unwarranted extension of its employment by those not recognizing its limitations has caused logicians to advance but cautiously its claims.

Reasoning by Analogy is the most primitive form of reasoning, and it certainly was the only form employed by primitive man, just as today it is the only form known to the undeveloped races, and, indeed, the only one used by untrained, uncultured minds even in civilized communities. It has a valid foundation in observation and experience; and, when a single-story structure is erected upon it, it frequently serves well its purpose; but when we attempt to build upon it a skyscraper, the rising structure frequently becomes insecure and often tumbles to the ground. Indeed, usually it is dangerous to build upon it a structure which rises above the ground-floor story.

Many valuable discoveries have been made through the principle of Analogy. Thus, a man who has mined gold in California, and who was then visiting in New South Wales, noticed that the mountains in the latter country were very similar in appearance to certain mountains in California in which he had dug gold. He, reasoning by Analogy, concluded that the mountains being alike in some respects, also should be alike in other respects; and so he dug for gold in them. His “guess” proved to be correct; he found rich ore in the hills, and the result was the great discovery of gold in Australia.

Geologists employed the principle of Analogy in their judgment that certain rocks were originally formed by processes similar to those observed to be in operation in the present period of the earth’s history. Noticing the marks on a sandy sea-beach from which the waves had just receded, they reasoned that the similar marks on certain rock-formations were produced in the same way at some early period of the history of the earth, the soft material afterward becoming hardened by natural processes. Seeing on certain rocks marks similar to those now impressed upon clay by raindrops and by the footprints of birds, mammals and insects, they reasoned that the markings on the rocks were caused in the same way, by prehistoric creatures, at some early geological period when the rocks were in a plastic condition.

In the same way, it is reasoned that the printed tables of Logarithms used by the Chinese were either copied from similar tables of the English, or else both had a common origin. The probability of mere coincidence was overcome by the discovery that certain errors in the English tables were duplicated in the ones used by the Chinese. The Analogy was so complete that the hypothesis of copying or a common origin was the only reasonable one. In the same way, it is reasoned that inasmuch as the planet Mars is found to have certain areas believed to be seas, and certain others believed to be land, therefore conditions on that planet must resemble to some extent those of the Earth.

Moreover, at each pole of Mars there is observed to be a white, rounded spot which is perceived to decrease in circumference when exposed to the sun’s direct rays, and to increase at other times, just as do the masses of ice and snow found around the poles of the Earth. Here the Analogy is so close that astronomers feel justified in believing that Mars has ice and snow at its poles, just as has the Earth. The same kind of reasoning has led to the belief that Mars has an atmosphere, with winds, clouds, rain and snow, very similar to corresponding phenomena manifested on the Earth. The reasoning, indeed, is often carried so far as to reach the conclusion that there is probably life of some kind on the planet Mars.

On the other hand, this form of reasoning often proves dangerous. For instance, the close resemblance between two kinds of fungus, or two kinds of fruit, may be so great as to cause persons to believe that they are practically identical; yet one class is wholesome food, the other class being poisonous. Or, “the other way around,” certain non-venomous serpents so closely resemble the venomous ones as to be mistaken for them. Children are often made ill or are killed by eating poisonous berries which they have gathered, and which they have mistaken for harmless berries of a similar appearance. Many persons have been killed by eating poisonous toadstools under the belief that they are mushrooms, the resemblance being very close. Jevons says: “In Norway, mushrooms are seldom seen, and are not eaten. Once when I was there, I found a few and ate them. I was afterward much amused by the people at the inn, who went out and collected toadstools and wanted me to eat them also. This was clearly a case of mistaken reasoning by Analogy.”

A physician visiting a patient discovers that there are present certain symptoms which are found in the early stages of scarlet-fever—the other symptoms not having as yet presented themselves. He reasons by Analogy that the missing symptoms are also proceeding to manifestation, and that this in all probability is a case of scarlet fever in its early stages. The scientist examining the fossil remains of an extinct species of animal, and finding that it possesses strong, blunt claws, reasons by Analogy that the creature had procured its food by scratching or burrowing in the earth. Buckland reconstructed an extinct animal from a few scattered fossil bones; the later discovery of an entire skeleton of the animal proved that his reconstruction had been absolutely correct in both generals and in details; this constituted a most successful example of reasoning by Analogy.

But, once more, there is always a great possibility of error in this form of reasoning. The dog, fearing a stick or a stone, will run away from you when you stoop suddenly to tie your shoe, to pick up a flower, or to turn over a peculiar leaf. It is cruel to reason by Analogy that because many drunkards have red noses, therefore all red noses are marks of habits of excessive drinking—the red nose of the quite temperate John Jones must not be taken as an evidence of dissolute habits. We have seen the danger of reasoning that a whale is “a fish” because it looks like one, swims like one, lives in the water like one. Halleck says: “Many false analogies are manufactured, and It is excellent training and practice to expose them. The majority of persons think so little that they swallow these false analogies just as newly-fledged robins swallow small stones dropped into their open mouths.”

The best thought today holds that true Logical Reasoning should be conducted along the lines ofInduction and Deduction, whenever this is possible in view of all the circumstances of the case; and that Analogy should be regarded as merely an imperfect form of these processes, or rather as a form of Imperfect Induction or Imperfect Deduction, and accordingly regarded as a makeshift to be employed only when true Induction or Deduction are impracticable under the particular circumstances of the case. At the best, Analogy is held to be but a “guess”—sometimes a “scientific guess,” or a “rational guess,” but still a “guess” at the last.

Here is the explanation of the employment by mankind of the principle of Analogy. Primitive man soon discovered that superficial resemblances existing between the various things of his everyday experience were reasonably sure evidences of a real inner and essential sameness between those things. One thing was found good to eat; therefore, another thing resembling it in appearance must be good to eat. Up to a certain point this form of reasoning was found to be correct. What was much more to the point with the primitive man, it was better than no reasoning at all. He knew absolutely nothing about certain reasoning based upon careful and extended observation, induction and deduction—these required more time and attention than he was able to bestow upon them, and, in fact, such more complex methods of reasoning never occurred to his mind. The degree of probability found in the results of reasoning by Analogy was sufficient to attract his attention, and to prove useful to him—so he was content, until he afterward discovered a better way—and that better way was really an evolution of the original way, after all.

It remained for the careful thinkers in advanced stages of the evolution of the race to discover that the principal value of Analogy is to be found in its suggestiveness; and that even where Analogy leads to the detection of truth and real facts it usually does so only when the observations or experiments upon which it is based have been sufficiently extended and carefully reasoned upon. It has been said: “Analogy may be applied with even reasonable confidence only when the degree of ascertained similarity is great, and when the extent of the preliminary observation is sufficiently wide.” Again, that: “Even where Analogy leads to the discovery of truth, the final establishment of such truth is never actually accomplished by Analogy, but really by some stricter logical method.”

Reasoning from Analogy results in merely probable conclusions; but the degree of probability may be raised to a high degree by pursuing the right methods and observing the proper precautions. Indeed, in the active affairs of ordinary life Analogy is really the only form of reasoning possible to most of us under ordinary existing circumstances, and we are very often forced to act upon conclusions reached only in this way. Reasoning by Analogy, carefully and cautiously exercised; has led to many important discoveries of natural science, mechanics, medicine, psychology, etc.; and it is often effectively applied in the practice of Law and in judicial decisions. In short: Analogy is useful (often necessary—frequently the only possible way); but its application must always be surrounded by the greatest care, and exercised with the greatest caution.

The essential distinction between Analogy and Induction is as follows: Analogy proceeds upon the general principle that, “A few things having many characteristics in common, also have other characteristics in common.” Induction proceeds upon the general principle that, “Many things having a few characteristics in common, all other things of the same class also have all these same essential characteristics.” Further, in Analogy we usually confine ourselves chiefly to the observation of the external and incidental characteristics of the several things in question; in Induction, however, we extend the observation and apply it particularly to the internal and essential characteristics of the things examined—we “go deeper into” the examination, and search for the essential elements.

The following diagram will illustrate the principal points of distinction between the processes of Analogy and Induction, respectively:

Examples: If we find that X has the characteristics known as a, b, c, d, e, f, respectively, and then find that Y has the characteristics a, b, c, d, respectively, we reason by Analogy that Y also possesses the additional common characteristics e and f, respectively, because these are found in X with which

• has so much else in common. Thus, finding that the planet Venus has the attributes of light, heat, water, and atmosphere in common with the Earth, we reason by Analogy that Venus probably possesses the additional attribute of “the presence of living things,” in common with the Earth—the latter having been found to possess it.

Induction, on the other hand, would reason as follows: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, (members of a general class of things) notwithstanding their great differences in many external and incidental characteristics, are found to possess in common the three internal and essential characteristics designated 1, 2, and 3, respectively; therefore it is probable that the remaining letters of the alphabet-class, viz., X, Y, and Z, also possess these three essential characteristics, notwithstanding that X, Y, and Z, manifest sundry differences in external and incidental characteristics from the remaining twenty-three letters of the alphabet-class.

Thus, finding that all known heavenly bodies obey the Law of Gravitation, the astronomer reasons by Induction that a newly discovered star must also obey that Law, though he has not as yet had time to examine its movements. Likewise, a chemist finding before him a transparent, colorless crystal composed of Carbonate of Lime, knows, by deduction based upon the Premises of Induction, that it will react to other stated chemicals in a certain definite manner; this because all forms of Carbonate of Lime, notwithstanding their external and incidental differences, have the internal, essential characteristic of such reaction.

The General Rule of Analogy, is as follows: “(1) The greater the number of points of discovered resemblance, the greater the degree of probability of the Analogy; the fewer such points, the less the degree of such probability. (2) The inferred additional points of resemblance become the more probable in the degree in which they are related to, or essentially connected with, those points of resemblance already established by observation and experiment. (3) Discovered points of essential difference often are sufficient entirely to destroy the presumption and inference of Analogy based upon many discovered points of external and incidental resemblance.”

We need scarcely consider in detail the many forms of possible application of the principle of Analogy; it is as familiar to you as is breathing or walking. You employ it in some form during almost every hour of your waking periods. It has its evident uses in forming everyday conclusions, opinions, judgments and decisions. You could not do without it, even if you so desired. The most that you can do in the matter of its application is to endeavor to employ it correctly, always recognizing its weak-points and dangers, and always observing carefully and consistently the above-stated rules concerning its degree of value and probability, its use, and its limitations.

Probably the best use of Analogy is that in which its conclusions are recognized as being merely tentative, i. e., adopted experimentally and for a trial, afterward to be subjected to more careful observation, examination and testing. By its employment in this way we often arrive at a valuable idea of a “probable cause,” or a “working hypothesis,” which afterward may be verified or disproved. Its reports must always be recognized as “probable truth,” never as “certain truth.” Jevons ably sums up the matter when he says: “In order to be clear about our conclusions, we ought never to rest satisfied with mere Analogy, but ought to try to discover the general laws governing the case. In Analogy we seem to reason from one fact to another, without troubling ourselves either with Deduction or Induction. But it is only by a kind of ‘guess’ that we do so; it is not really conclusive reasoning. We ought properly to ascertain what general Laws of Nature are shown to exist by the facts observed, and then to infer what will happen according to those Laws. … We find that reasoning by Analogy is not to be depended upon, unless we make such further inquiry into the causes and laws of the things in question which really necessitates the employment of Inductive and Deductive Reasoning.”

The Law of Logical Induction

You are now invited to consider that important Law of Logical Reasoning known as the Law of Logical Induction. This Law represents the universal experience of human thought rationally applied and directed. The Law of Logical Induction is expressed in the fifth of the Seven Axioms of Logical Reasoning, which is as follows:

1. THE AXIOM OF LOGICAL INDUCTION: “What is discovered to be true of a great number of observed objects, things or individuals of a definite general class, is practically certain to be true of that general class as a whole; the characteristics assumed to be possessed in common by all the individual objects or things in a definite general class, constitute the accepted essential characteristics of that class as a whole.” This fundamental principle of Induction has been stated in many forms, among which are the following: “What is true of the many, is true of the whole.” “That which belongs or does not belong to many things of the same kind, belongs or does not belong to all things of the same kind.” Mills’ statement of the Principle of Induction is very comprehensive; it is as follows: “Induction is that operation of the mind by which we infer that what we know in a particular case or cases will be true in all cases which resemble the former in certain assignable respects. In other words, Induction is the process by which we conclude that what is true of certain individuals of a class is true of the whole class; or that what is true at certain times will be true in similar circumstances at all times.”

In the early days of Logic, the principle of Induction was largely neglected by reason of the great emphasis placed upon the principle of Deduction. The followers of the old philosophies and systems of Logic, which were fathered by Aristotle and long afterward wet-nursed by the Scholastic School of Philosophy, and which for many centuries dominated the world of logical thought and philosophy, believed that it was possible to arrive at all human knowledge by the methods of Formal Logic applied along the lines of Deductive Reasoning. The Syllogism was elevated to the highest rank, and logicians bowed down before it and worshipped it. As Jevons says: “Men preferred trusting to Aristotle, rather than using their own eyes.” Of course, it was necessary to find bases for the Premises employed in such Deductive Reasoning, and a certain degree of Induction was employed in finding these. But, at the best, but Imperfect Induction, or a sublimated form of Analogy, served the purpose in most cases; in other cases, resort was had to “A Priori” Judgments, i. e., Propositions assumed to be true more or less independent of extended observation, experiment, or wide experience—more often held to be “innate ideas” or “universal intuitions.” Logicians reasoned from assumed causes to effects, but too often without first being sure that the assumed causes were real causes. They ignored “A Posteriori, reasoning, i. e., reasoning proceeding from effect to causes—Judgments based upon experimental proof. They contented themselves with deducing particular facts from assumed general principles; they neglected the correlated logical process of reasoning by Induction from particular facts to general principles—and thus assuring themselves of the validity of the general principles which formed the bases of their deductive processes.

The rise of Inductive Reasoning to its proper place was due in a great measure to the influence of Roger Bacon (A. D. 1214­1292) and of Francis Bacon (A. D. 1561-1629); the former laid the basis, the latter advanced the idea and formulated methods of applying the principles. Francis Bacon is often styled “The Father of Inductive Reasoning and the Founder of the Scientific Method”; but the preliminary work of Roger Bacon must not be overlooked nor forgotten. Today, practically all scientific thought is based upon the conclusions reached by Inductive Reasoning. The Physical Sciences would perish were this principle eliminated; even modern Psychology is based upon it.

Modern Logic gives Inductive Reasoning a high place; indeed, there are learned logicians who even go so far as to claim that Deductive Reasoning is but a reflection of Inductive Reasoning, and that Deduction usually is but a re-statement of the conclusions already arrived at through Induction— but here the truth probably lies between the two extremes, and Induction and Deduction are seen to be correlated and coordinated processes of Logical Reasoning.

In our consideration of the subject of Logical Synthesis, or Classification, we have shown you how and why individual objects possessing certain common characteristics are grouped or “generalized” into classes; the common characteristics of all these individual objects thus becoming the “essential characteristics” of that class. The same principle, as you have seen, governs the grouping or “generalization” of these classes into larger classes, and so on. We now ask you to make note of the fact that all such Logical Synthesis, Classification and Generalization proceeds according to the Law of Logical Induction. It is governed by the principle that: “The characteristics assumed to be possessed in common by all the individual objects or things in a definite class, constitute the accepted essential characteristics of that class as a whole”— such characteristics become the “essential elements or qualities” of the Concept representing that general class of particular things or individual objects.

But, no matter how many may be the individual objects or particular things of the general class which have been observed and examined for the purpose of ascertaining whether or not they possess the certain necessary characteristics deemed essential to the class, it is practically impossible that all such individual objects and particular things can be so observed and examined in the great majority of cases. In fact, it is almost certain that in most cases there are far more not so observed and examined than are so treated; this, because of the natural limitations of man’s powers of observation, experiment and, inspection.

Hence, usually the Law of Induction bases its conclusions upon human experience with the many rather than with the all of a class of things and objects. This fact is expressed in the axiom, as follows: “What is discovered to be true of a great number of observed objects, things or individuals of a definite general class, is practically certain to be true of that general class as a whole.”

If all the individual things and particular objects in a certain class are observed, subjected to experiment, and found to possess certain characteristics in common, then the Judgment must be that these common characteristics absolutely and certainly are the “essential elements or qualities” of that class, and of its associated Concept. But when only “a great number” of such are observed, inspected,and found to possess such common characteristics, then the Judgment must be merely “practically certain,” i. e., possessing a high degree of probability of truth.” In very many cases, it is true, this high degree of probability falls but little short of absolute certainty.

All that Inductive Reasoning may truthfully claim is to announce principles, laws and judgments which for all practical purposes of life may be considered as true and certain. But this is likewise true of all forms of Logical Inference, or human reasoning; even Deductive Reasoning, with its boasted formal “certainty,” must be based upon Premises assumed to be true by the principles of induction: it is always a case of “so-and-so is true, if such-and-such be true.” Naught but Omniscience could reason with absolute certainty; and Omniscience would not need to “reason,” for it would already know all that is possible to be known—Reasoning is but the method employed to “find out” and know something that is not known.

In the light of the foregoing statements concerning the possibilities, probabilities, and natural limitations of the Principles of Inductive Reasoning, let us now consider the general methods employed in conducting its processes. Inductive Reasoning proceeds according to the following steps or stages, viz., (1) Preliminary Observation; (2) Making the Hypothesis; (3) Verification by Testing. Each of these respective processes are described in further detail in the next following pages of this section of this book.

1. Preliminary Observation. In this process preliminary to that of actual Inductive Reasoning, there is conducted an examination of a great number of individual objects or particular things believed likely to belong to a certain general class of things, activities or events. Such examination is for the purpose of ascertaining definitely the common characteristics of such things, in order to decide whether or not these constitute the “essential elements or qualities” of that class as a whole. Usually, a more or less general classification, based upon Logical Analogy, or Imperfect Induction, has preceded such test, trial or experiment. Observation and Experiment, however, do not constitute Induction; they merely supply Induction with its working material.
2. Making the Hypothesis. In this process of Inductive Reasoning, there is performed the mental action of combining into a general idea (akin to a Concept) the total results of the extended series of observations and experiments which have preceded this stage; and of representing this general idea in the form of what is known as an Hypothesis, i. e., “A supposition, proposition or principle assumed or taken for granted in order to deduce therefrom particular proofs.”

Hypothesis is the simplest term indicating the result of Inductive Observation and Experiment. Theory is held to be a stronger term, and usually indicates an Hypothesis which has been verified at least to some extent by subsequent observation. A Law is an Hypothesis or Theory raised to a very high degree of probability by reason of extended and positive observation and experiment. A Principle is “a Law of Laws,” or “the Reason of Laws,” or a Universal Law including in its content several subordinate Laws which are governed by its essential characteristics and powers.

A Law, from another viewpoint, may be said to be: “A general rule of procedure according to which things move, act, and work”; a Principle being: “That by reason of which change-producing actions and motions proceed, and in which they have their source.” But the latter two terms, Law and Principle, respectively, have a wide range of meaning, are subjected to varied interpretations and definitions, and are applied to many different general ideas; we give here merely their respective meanings as usually understood and employed in Logic, Physical Science and Psychology.

Hypotheses, as might be supposed, possess varying respective degrees of validity or probability. Some are merely “tentative,” or “‘working hypotheses” employed for convenience of thought and further investigation; others rise to the dignity of verified Theory, or perhaps even to the high rank of Laws and Principles. The following general rule is usually employed by logical, scientific thinkers to determine the respective value and strength of Hypotheses.

Rule for Valuation of Hypotheses: (1) If the Hypothesis involves only a few essential characteristics of its class, it must be supported by a much larger number of particular observations and experiments than if it involves a greater number of such. (2) The greater the number of facts and phenomena satisfactorily accounted for by an Hypothesis, the greater is its probable validity. (3) Where there is more than one Hypothesis claiming recognition as the explanation of a series of given facts or phenomena, then that one which is found to account for the greater number of such effects is to be considered as the most probable, all else being considered.

• Where more than one Hypothesis is so advanced, each one of which seemingly possessing equal value, then further observation and experiment is necessary; a later stage of the inquiry will probably uncover and reveal certain additional facts which are explainable only by one particular Hypothesis, and not by the others; or possibly one such Hypothesis may be found to include the others as minor and constituent factors or elements.
• VERiFiCATioN by In this process of Inductive Reasoning, there is performed a subsequent investigation in which there is “tested out” the application of the tentatively adopted “working hypothesis” to additional particular cases, or to new individual objects and things. The test is conducted for the purpose of ascertaining whether or not the Hypothesis “works out” satisfactorily in such application. Each case in which it is found to “work out” satisfactorily tends to strengthen it. But if there are found one or more cases in which it will not “work out” satisfactorily (provided that the failure cannot be accounted for or explained away logically and rationally) it is weakened to that extent; if such failures are numerous, the result may be the rejection of the Hypothesis in question, though, here, allowance must always be made for possible disturbing causes, and a search for these should be conducted— experience having demonstrated the need of such precaution.

The process and method of Verifying an Hypothesis have been humorously illustrated by the story of Cinderella. The Glass Slipper constitutes “the facts of the case”—it symbolizes the given series of phenomena. Cinderella is the Hypothesis— or, rather, one of the Hypotheses, for each one of her rival sisters is also an Hypothesis. The process of testing for verification consists of trying the Glass Slipper in turn on the feet of the several rival candidates. The Hypotheses of the rival sisters are each found invalid—the Glass Slipper will fit the foot of none of them, even though they cut off their toes and heels in order to “make the facts square with the theory,” When, however, the Cinderella Hypothesis is tested by applying it to the facts of the Glass Slipper, lo! the “fit” is found to be perfect—the hypothesis is verified, and raised to the rank of a Verified Theory; later, when Cinderella marries the Prince, it may, perchance, be elevated to the exalted position of a Law, or even that of a Principle!

Rules of Verification.

The test of Verification is not merely simple observation, but rather “experimental observation,” i. e., observation resulting from “a test, trial, or experiment” conducted on scientific principles, in which the possibilities of error are largely eliminated.

The success of the test, trial and experiment is determined by the proportion of cases found to be explainable by reason of the Hypothesis; the greater the number of cases so explained and accounted for, the greater degree of probability and validity must be attached to the Hypothesis, and the more perfect will be deemed the Induction. The “facts” and the Hypothesis must agree with each other; the greater the agreement, the greater the probability, validity and degree of verification.

A reasonable number of failures is usually sufficient to discredit an Hypothesis, unless such can be explained by the presence and action of a disturbing agency. Once, a promising theory of Astronomy was seemingly discredited by the erratic movement of a certain planet; later a “disturbing agent” was detected in the form of a certain previously undiscovered planet which had served to pull the first-named planet out of place; the discovery of the new planet explained the discrepancy, and cancelled the evidence against the theory.

If the Hypothesis is found materially wrong, and therefore discredited, two alternative courses are open, viz., (1) to discard the Hypothesis, and then to seek for a new and better one; or – to modify the faulty Hypothesis in some minor degree, and to then test it once more in its new form—this frequently cures the trouble, and settles the matter satisfactorily.

The Law of PARSiMoNY. The Law of Parsimony, carefully applied, often results satisfactorily in deciding between two or more promising Hypothesis. This Law is stated as follows: “(1) Explanations should not be unnecessarily extended, multiplied or complicated; but should be limited so far as is possible, and rendered simple so far as is possible. (2) All else being equal, a simple explanation should be preferred to a complex one; a limited explanation, to a more extended one; a close, ready, immediate explanation, to a remote one. (3) An unknown must not be accounted for or explained, by one still less knowable, or still more unknown, when a known explanation is at hand.” The Law of Parsimony has also been called “The Law of the Economy of Thought.” It is a valuable and efficient, though comparatively little known, principle of Logical Thought. We advise you to commit it to memory, and to apply it.

The Law of Logical Causation

You are now invited to consider that important Law of Logical Reasoning known as the Law of Logical Causation. This Law represents the universal experience of human thought rationally applied and directed. The Law of Logical Causation is expressed in the sixth of the Seven Axioms of Logical Reasoning, which is as Follows:

1. THE AXIOM OF LOGICAL CAUSATION: “Every change, happening, event, or entrance into or exit from existence, proceeds from precedent conditions or causes; given the same causative factors, the same material elements, and the same environmental conditions, the same results and effects will follow in all cases so determined and conditioned.”

This axiom states a truth which is verified by all human experience, is supported by the common-sense reports of the race, and is substantiated by the judgment of the keenest logical and philosophical thought. It is regarded as self-evident truth, and as a proposition which may be taken for granted; it is assumed in all logical thought, and is implied in all true reasoning. The following consideration is not intended to be offered as proof of its truth; but is designed merely to elucidate and make clearer the manifestation of this principle in the world of thought and things.

The Law of Causation is expressed in popular terms as follows: “Everything that happens is the result of a Cause; without a Cause, nothing happens.” A more technical statement is: “All changes in things, and, therefore, all actions, movements, events, happenings, and occurrences involving change, are the results or effects of certain antecedent activities, conditions, forms or states of things, known as Causes. These Causes being present, the results and effects must occur; these Causes being absent, the results and effects cannot occur.”

The following statements of technical, authoritative writers of the subject may serve to illustrate further the natural principle operating through this law:

Jevons says: “The Cause of an event means the circumstances which must have preceded in order that the event should happen.” Baldwin says: “Every event is the result or sequel of some previous event, or events, without which it could not have happened, and which being present it must take place.” McGilvary says: “Causation is the relation of Cause to Effect. The Cause of any event is a preceding event without which the event in question would not have occurred. Both Causes and Effects are always events; not things, but things in action. The complete Cause would be all the indispensable previous events. But as all inquiry that is of any value is confined within limits, the question as to the Cause of an event is not generally a demand for the complete inventory of indispensable previous events, but some event which, in connection with other events, taken for granted, is needed to account for the event under discussion.”

If we deny the Law of Causation, we may as well deny the existence of all Natural Law and Order; for Natural Law and Order cannot proceed from Chance, but is clearly the manifestation of the Law of Causation. A Law is “the way things act and proceed”; and all things are discovered to act and proceed according to orderly sequence and logical order: this universal fact attests the validity of the Law of Causation.

The ancients employed the term, “The Cosmos” to indicate “the World conceived as proceeding according to Law and Order”; the opposite conception and term being that of “Chaos,” or “The World conceived as lacking Law and Order, and hence, the World conceived as existing in a state of lawlessness, disorder, and confusion.” The position of modern science is that so forcibly expressed by one of its pioneers in the axiom: “The Universe is governed by Laws.” The only alternative is the conception of a World of Chance. The latter is unthinkable in view of the discovery of the constant and invariable operation of the Law of Causation in the Universe.

Logical thought recognizes the existence of “Chance” only in the sense and signification of, “The unknown, unperceived or remote Causes of an event.” It denies the existence of “Chance,” in the sense and signification of, “Absence or lack of Causes.” A leading reference work says: “Chance is a word which in its original and strict meaning may be defined as the causelessness of an event. But with the growing insight into the universal prevalence of Causality, Chance in this sense of the term is no longer regarded as possible. The word continues to be used in a different sense, viz., the unknown cause or causes of an event. The cause or causes may be entirely unknown, or unknown only in detail. In either case there is a lack of predictability; and in so far as an event is unpredictable it is said to be due to Chance. The unpredictable event is itself called ‘an accident,’ sometimes also itself ‘a chance’.”

You will notice that in the Axiom of Causation is stated that not only “every change, happening, or event,” but also “every entrance into or exit from existence” comes under the Law, and “proceeds from precedent conditions or causes.” An event is “that which comes, arrives, or happens.” Events arise from and are accompanied by changes in things. Every change in things implies a Cause or Causes producing the change; it is logical to posit a necessary Cause to account for every change.

Now, “every entrance into or exit from existence” is a change, or “becoming”; consequently every “coming into existence” or “exit from existence” must have its Cause. But, note this important fact: If there be posited a Something or Somewhat which is Eternal, and which, therefore, has never “come into existence,” or “entered into existence,” or “become existent,” then the existence of that Something or Somewhat does not imply the necessary precedent existence and action of a Cause; and, logically, we have no right to demand a Cause for such.

Consequently, each and every school of philosophy, metaphysics, or theology equally is entitled to be absolved from the necessity of “explaining by Cause” the fact of the existence of its own particular posited Eternal Ultimate Principle, Law, Process, or Being, upon some one of which all philosophies, systems of metaphysics and theologies base their respective reasoning. If there exists anything that is Eternal, then such thing must of necessity be Causeless. Only that which is conceived as “coming into” or “entering into” existence requires the positing of a Cause to explain such “becoming.” As Bowne says: “It is not existence as such that demands a Cause, but a changing existence. * * * It is entrance and exit only that give rise to this demand. Whatever manifests them must have a Cause; whatever does not manifest them can dispense with a Cause.”

However, in this particular instruction we are dealing only with Natural Things; things which become objects of perception and conception. All such things are temporal things; things which have come into existence, which manifest constant change during their period of existence, and which are destined to pass out of existence, all through a process of “becoming.” Such things, then, are clearly under the Law of Causation. In the present consideration, therefore, we are dealing only with things that come, dwell a while, and then go—all under the Law of Change, and therefore, under the Law of Causation.

The importance of the Law of Causation is realized more fully when it is recognized that in the Cause or Causes of an event, happening, change or entrance into existence, are to be found the “because,” “reason,” and “explanation” of the occurrence. When you know the Cause or Causes, then you are aware of the “reasons” explaining and accounting for the Effect or Result. When you say that such-and-such a thing happened because of so-and-so, then that “so-and-so” represents the Cause or Causes because of which the thing happened, occurred, changed or made its entrance into existence—or passed out of existence. So, you see, there are great principles involved in the Law of Causation.

The application of the principles of the Law of Causation in Logical Reasoning is performed chiefly in certain phases of Inductive Reasoning, which form the subject of the preceding section of this book devoted to the consideration of the Law of Induction. Inductive Reasoning is actively concerned with the discovery of the unknown Causes of known effects and results—of known events, happenings, changes, entrances into and exits from existence—in short, with the relations of Cause and Effect existing between all things. At that point of our instruction in which Inductive Reasoning was considered in detail, your attention was directed to the general laws and principles involved in that form of Logical Reasoning. However, at this point, we think it proper to call your attention to some special rules observed by trained reasoners in those processes of Inductive Reasoning having to do With the operation of the Law of Causation.

Difficulties of Discovering Causal Relations.

The following general classes of difficulties experienced in determining the relation of Cause and Effect manifesting in correlated things should be carefully noted by you. Frequently, the knowledge of the precise nature of the difficulty will prevent you from committing a fallacy of reasoning, or from indulging in False Reasoning, along these particular lines; it will also serve to indicate at least the general direction in which lies the true solution of some difficult problems arising in the study of Cause and Effect.

1. Causes Beyond Experience. Where the Cause lies outside of human experience, or at least out of the experience of the individual, and is therefore not to be comprehended or understood, the remedy is: (1) if it be found that while one’s individual experience does not include the possible knowledge of the unknown Cause, then he should seek the solution in the experience of acknowledged authorities on the subject in question—care, however, being taken to satisfy himself that the authority actually is possessed by those claiming it or reputed to possess it, rather than depending merely upon their unwarranted and impudent assumption of it, or upon the uncritical judgment of those who attribute it to such persons;
2. if it be found that the knowledge of the unknown Cause necessarily lies out of all human experience, then the question should be put aside, because the mind is unable to apprehend any knowledge other than that originally based upon human experience; failure to act upon this principle results merely in circular reasoning—the mind traveling about like the squirrel in his wheel, ever moving but never really advancing.
3. Joint Causes. Where there are two or more Causes acting conjointly, thereby rendering it difficult to determine which is the predominant Cause, or to eliminate from the problem the associated Causes, then the remedy is to observe other cases in which some one of the several possible Causes has by itself operated to produce similar results independent of the other possible Causes. If any one of the said possible Causes is found to be capable of producing an Effect identical with or quite similar to the Effect under observation (without the possible presence or action of the other possible Causes): and where the other possible Causes are not found to be capable of so producing such identical or similar Effects; then it is logical to reason that the successful possible Cause is the true Cause. In the absence of such decisive result of the test, you must either label the question as “undecided,” or else tentatively assume that the Effect is the result of the several possible Causes necessarily acting conjointly. Tests along these lines will frequently eliminate certain of the factors as non-essential in the joint action, thus narrowing the unanalyzed combination to the remaining factors.
4. Modifying Where there are found to exist some modifying or counteracting Cause or Causes, which tend to confuse the investigator and to cloud the result of his investigation, then the remedy is that of Elimination (see the below stated rule of Elimination).
5. Plurality of Possible Where there are found present and active several possible Causes, either of which seems to be sufficient to account for the Effect, then here again the remedy is found in Elimination (see the rule stated below).
6. Cause or Co-Effect. Where to the casual reasoner there seems to be found in a supposed Cause the sufficient explanation of the Effect; but where to the more careful reasoner the supposed Cause appears to be possibly merely a co-Effect of the true unknown Cause rather than that true Cause itself, then here again the remedy is that of Elimination (see the rule stated below).
7. Where the apparent relation of Cause and Effect is seen probably or possibly to be the result of mere Coincidence, the relation of Cause and Effect probably or possibly being merely a relation of Time and Place arising from a concurrent happening, i. e., a happening at the same time and in the same place, though without any true logical relation of Cause and Effect existing between the respective happenings, then once more the remedy is found in Elimination (see the below stated rule).

Reversal of Relation.

Where the apparent Cause is suspected really to be the Effect, and the supposed Effect really to be the Cause, then the remedy lies in testing the apparent Cause and the apparent Effect apart from each other, and under different conditions. In such case, careful observation and experiment are necessary.

Rule of Elimination.

The Rule of Elimination (above referred to in several cases) is as follows: “Test each possible or probable Cause separately, and apart from other possible or probable Causes of a certain Effect, with the end and purpose of eliminating from the problem such apparent Causes which may be discovered to be incapable of meeting the logical causal requirements of the case, which requirements the True Cause must fulfill. The particular possible or probable Cause which is left after all the others have been eliminated (provided that it, itself, successfully meets the requirements of the case) is then to be accepted as the true Cause—at least so long as no other candidate for the office of True Cause, also meeting the requirements, presents itself and challenges the holder of the office.”

Illustrations of Elimination.

The following examples serve to illustrate the Rule of Elimination which, in one form or another, is employed by the most careful thinkers.

1. A gun is discharged. The savage tries to fire it again, while still unloaded. He fails. He then places a shell within it, and finds that it “goes off.” Henceforth he eliminates the unloaded gun from the category of possible Causes or Casual conditions of “gun-firing.”
2. A person is made sick by something eaten at a dinner, but he does not know just which particular dish was tainted. He proceeds to test the thing by Elimination. He remembers that he ate soup, meat, fish, bread and vegetables. He discovers that a number of other persons also were made sick at that dinner; while others still were not so affected. He examines the latter class, and finds that all of them ate meat, and that some of them ate soup and bread, or vegetables, as the case might be. He eliminates all of these articles of food as probable factors of the illness, by reason of the fact that many of the well persons had eaten of each. When he reaches the item of fish, however, he finds that none of the well persons had partaken of it. Further inquiry reveals the fact that all of the sick persons had eaten it. He reasons from this that the fish was the tainted article of food which caused his sickness. If he alone had been made sick, his test would have shown either (a) that his particular portion of some article of food had been tainted, or (b) that his stomach was in bad order, or (c) that some particular combination of food had disagreed with him by reason of some personal idiosyncracy. We have here several elements of possible Cause and Effect, and the detection of the True Cause. Try to discover each—it will give you good practice and exercise.

3. Nitro-glycerine is discovered to be explosive. A man wishing to discover the prime explosive factors of the composite article tried separately the several constituent ingredients, i. e., glycerine and the nitric and other acids which composed it. He found that none of the several separated ingredients exploded, and that no other than a certain special combination of these exploded. In the case of many explosives, the explosion occurs only when the several ingredients are combined in certain proportions. Hence the conclusion that all of these factors, in certain combination and coordination, are the necessary factors of the cause, and constitute the True Cause of the Effect.
4. A man finds that his cup of tea is bad. He tries the experiment of using a different brand of tea, boiling it in the same kind of water; this results in another bad cup of tea. He then separately tries both brands of tea, using a different kind of water from that first used; both cups are found good. He decides that something was wrong with the water, and that the water was the True Cause of the Effect.
5. A scientific man fills a receiver full of air, and causes a bell to ring within the closed receiver; he hears the sound. Then he exhausts the air from the receiver, and causes the bell to swing; he hears no sound. Hence he reasons that the Effect (i. e., the sound of the bell) which was present in one case, and absent in the other, resulted from the discovered essential Cause (i. e., the presence of their air which conducted the sound-waves).

6. A man finds a room well lighted; he notices a number of peculiar glowing globes about the room (he had never seen an electric light lamp before). He experiments by turning off the globes, one after the other; and then turning them on again, one by one: he finds that the light in the room decreases by reason of the first action, and increases by reason of the second. Therefore he reasons that the peculiar glowing globes are the True Cause of the light in the room.
7. A man weighs a barrel filled with flour; he finds that it registers 210 pounds. He knows that the empty barrel alone weighs 14 pounds. He reasons that he has 196 pounds of flour in that barrel, which is the Cause of that part of the Effect which was not attributable to the barrel.

“These are trifling examples and illustrations,” you may say. Well, they are so, provided that you fail to grasp the basic principle involved in each. But these basic principles are precisely the ones employed by the great scientists, and by reason of which they have made their great discoveries of Laws and Principles. Perhaps, however, you may grasp these principles better when we present to you illustrations of certain Fallacies resulting from a failure to apply them. Here are a few familiar and typically illustrative cases involving such Fallacies.

1. Mistaken Causes: The rooster thought that his crowing caused the sun to rise; because, always just after he crowed, up came the sun. His fallacy was exposed when one day he overslept himself, and the sun rose without his crowing. Again: In ancient times, from the coincidence of the simultaneous appearance of a comet and an epidemic of the plague, it was reasoned that the comet was the cause of the plague. The fallacy was exposed when it was shown that other comets had appeared without the coincident appearance of the plague; and likewise, that other plagues had appeared when no comet accompanied them. Again: A child reasoned that because deaths in that town were always preceded by the visits of a physician, therefore, the doctors were the Causes of the deaths. You may expose this fallacy for yourself. Again: Ignorant and violently prejudiced people have sought to attribute the occurrence of bad crops, unfavorable seasons, bad weather in harvesting season, etc., to the fact that a particular political party happened to be in power. You may smile at this, but cases of this kind actually have been experienced. Other cases just as silly are those in which a certain administration, or political party in power, has been held to be the Cause of things which were utterly beyond its power to affect one way or another, and which proceeded from entirely different Causes.

1. Confusion of Cause and Effect: Some ignorant persons think that the eruptive pimples which are the symptoms of certain diseases are really the Cause of the disease instead of its Effect. Again: It might be argued that silk-hats are the Cause of Civilization, because the greater the degree of Civilization the greater the number of high-hats appearing on the streets. Again: that, for the same reasons, automobiles are the Cause of Prosperity instead of an Effect of it. Again: that, for the same reasons, straw hats are the cause of hot weather. Again: that certain royal personages were the respective Causes of the high degree of culture, prosperity and progress during certain periods, instead of their being merely incidental and coincidental facts—this is quite a common fallacy.

The foregoing examples may seem to be absurdly exaggerated cases of Fallacy of this kind; but others of the same general character, and equally contrary to reason, are being manifested by presumably intelligent persons every day in the year—and often are undetected and unexposed. When you train your mind along the lines of Practical Logic, you will by habit escape perpetrating these offences against Logical Reasoning, and will instinctively recognize and detect such when seriously and solemnly advanced by others. This is quite “worth while,” is it not?

The “Jevons’ Rules” of Discovery of Causes and Effects. Concluding our consideration of the subject of the application of the Law of Cause and Effect, we would call your particular and especial attention to the well-known, generally accepted, and very practical and useful rules laid down by Professor Jevons, that eminent teacher of Logic, which rules will serve to aid you in discovering and identifying true cases of Cause and Effect. These rules are as follows:

1. “Whenever we can alter the quantity of the things experimented on, we can apply the following rule for discovering which are Causes and which are Effects, viz.: Vary the quantity of one thing, making it at one time greater and at another time less, and if you observe any other thing which varies just at the same times, it will in all probability be an Effect.
2. “When things vary regularly and frequently, there is a simple rule by following which you can judge whether changes are connected together as Causes and Effects; this rule is as follows: Those things which change at exactly the same times are in all likelihood connected together.”

The above, and the previously presented rules, when applied by Common Sense and according to Experience, will render you an efficient reasoner along the lines of the relations of Cause and Effect—and such lines really extend over a vast field of your practical thought. Knowledge of the Causes and Effects of things under consideration is sometimes the most valuable of all possible knowledge.

The second, and concluding, part of the Axiom of Logical Causation states: “Given the same causative factors, the same material elements, and the same environmental conditions, the same results and affects will follow in all cases so determined and conditioned.” This principle is so intimately and absolutely bound up with, correlated to and coordinated with, the first principle announced in that axiom, that it inevitably, invariably and infallibly follows as an absolute necessity of the truth of the former; the two cannot be divorced. Reason has joined these two together so firmly that they cannot be put asunder. To deny either, or both, is equivalent to asserting the reign of Chance, rather than that of Law and Order—to regarding the Universe as Chaos, rather than as the Cosmos.

This truth is expressed in many strong phases employed by eminent thinkers. For instance: “From the same Causes, the same Effects proceed”; “What is true at certain times, under certain conditions, will be true under similar circumstances at all times.” It is based upon the realization that Nature proceeds according to fixed and certain Law—according to a uniform, constant, invariable routine and sequence of Orderly Trend; that the Universe is governed by Law, and not by Chance, and proceeds according to Rule, and not in any “higgledy-piggledy,” irregular, nonuniform course. If we deny the validity of Natural Law, we may as well stop thinking at all, for the most important part of our thought is based upon the conception and premise of Universal Law and Order.

We are justified in believing in “Nature’s Common Course,” for all experience supports such belief, and all Logical Reasoning verifies it. It has been said that: “We do not ask for the reasons of this uniformity—we cannot help believing in it even if we try not to do so.” It is a “necessity of rational thought.”

The Law of Logical Deduction

You are now invited to consider that important Law of Logical Reasoning known as the Law of Logical Deduction. This Law represents the universal experience of human thought, rationally applied and directed. The Law of Logical Deduction is expressed in the seventh of the Seven Axioms of Logical Reasoning, which is as follows:

AXIOM OF LOGICAL DEDUCTION:

“What is true of the class as a whole, must be true of each, every and all the individuals composing that class.”

The principle, law and truth embodied in this axiom is employed in all Logical Reasoning. It is regarded as self-evident truth, properly to be taken for granted; it is assumed in all logical thought, and is implied in all true reasoning. The Law of Logical Deduction from the earliest times has been recognized and employed in Logical Reasoning. In fact, until the rise into favor of Inductive Reasoning the logicians held that Deduction was the only valid form of logical inference. At present, it is clearly perceived that inasmuch as the material for all Deduction must be furnished ready-made by Induction, and inasmuch as Induction must be verified by subsequent Deduction, consequently, these two great forms of Logical Reasoning can not be divorced one from the other.

Some ardent advocates of Inductive Reasoning, in fact, go so far as to claim that Deduction is really nothing more or less than a method of making practical application of the results of Induction; and that the conclusions reached by Deduction have been previously implicitly asserted in the judgments passed upon the individual objects when they are admitted into their respective logical classes. We shall, however, not enter, here into such technical discussion, particularly as we believe that in this, as in most cases, the truth is to be found in the middle course—between the two extremes.

Deduction is the logical process whereby we deduce by inference an unknown particular truth from two already known general truths. As has been said by an eminent logician, it is “getting some knowledge from other knowledge.” Again, it has been stated as, “finding out what is true if certain other things are true.” Examples of Deduction follow: “All men are mortal; Socrates is a man; therefore, Socrates is mortal.” “All horses are animals; this creature is a horse; therefore, this creature is an animal”, “All magnets attract steel; this piece of steel is a magnet; therefore, this piece of steel will attract other steel.” “All mushrooms are good to eat; this fungus is a mushroom; therefore, this fungus is good to eat.” “No fish is a warm-blooded mammal; the whale is a warm-blooded mammal; therefore, the whale is not a fish.” “All A is B; this thing is an A; therefore, this thing is B.”

In the above-stated examples you fin d that there are two already-known facts—two Propositions, two judgments: these are called the “Premises.” There is also a third fact, a newly discovered fact—a third Judgment; this is called the “Conclusion,” or “Deduced Judgment.” A Premise is: “A Proposition antecedently supposed or proved, from two of which a Conclusion is drawn by Deductive Inference.” The most general of the two Premises is known as the Major Premise; the less general is known as the Minor Premise. For instance, in the classical illustration, the Major Premise is: “All men are mortal; the Minor Premise is “Socrates is a man”; the Conclusion is “Socrates is mortal.”

The Syllogism.

To the average student one of the most forbidding things revealed in Formal Logic is that bearing the unfamiliar name of the “Syllogism.” The name itself seems to suggest terrifying possibilities in the form of technicalities and academic hair-splitting; and a cursory examination of the distinction between the manifold forms of the Syllogism is calculated to add to this feeling of apprehension. But, really, the only difficult feature of the Syllogism (in its simpler forms, at least) is its name. As a matter of fact, you use Syllogism every day in your ordinary thinking, and have always done so, though perhaps you have not realized the fact.

A Syllogism is simply: “The regular logical form of every logical argument or process of Deductive Reasoning.” Each of the examples given above to illustrate the principle of Deduction is a Syllogism. The classical example is: “All men are mortal; Socrates is a man; therefore, Socrates is mortal.” Each Syllogism consists of three elements, viz., the Major Premise, the Minor Premise, and the Conclusion. The Major Premise contains the most Universal term (in the above example, this is “mortal”). The Minor Premise contains the most Particular term (in the above example, this is “Socrates”). The Conclusion contains the most Particular term as its subject, and the most Universal term as its predicate (as, for instance, “Socrates is mortal”). There is also a “middle term” which does not appear in the Conclusion, but which appears in the Minor Premise and the Major Premise (in the above example the “middle term” is “Man” (or “Men”).

The Major Premise of a Syllogism has been previously arrived at by means of Induction. The Minor Premise is the result of previous Induction or Deduction, as the case may be. The Conclusion is the Judgment obtained by the present process of Deduction. The three elements of the Syllogism are known as “Propositions.” A Proposition is: “A Judgment between two Concepts, formally expressed in words.”

You may think that the idea of the Syllogism is purely technical and artificial, having nothing to do with “plain, practical everyday thinking”; but if so, you are mistaken. You employ the Syllogism constantly when you think in the form of reasoning, argument, or decision; though you employ it more or less unconsciously. When you see a wasp moving toward you, you seem to say to yourself merely, “I must look out for that wasp”; but your mind really is thinking (though for the most part more or less unconsciously) “All wasps sting; that insect is a wasp; therefore, that insect stings.” If it were not for your previously acquired knowledge of your Major Premise, i. e., “All wasps sting”; and of your Minor Premise, i. e., “That insect is a wasp”; you would not be able to arrive at your (more or less unconscious) Conclusion, i. e., “That insect stings,” which, in turn arouses your desire and will to “look out for that wasp.” You follow the same general course when you move away from the place at which you hear the rattlesnakes’s warning. You follow it when you retreat rapidly from the presence of the skunk—though you do not stop to analyze your thought into its elements, or to translate it into words. You follow it when you gently lay down the stick of strange looking substance when someone calls out to you: “Look out; that is dynamite.” You use it when you “know” that a particular pauper pays no taxes; though your mind only unconsciously goes through the thinking stages of “He is a pauper; paupers do not pay taxes; therefore, he does not pay taxes.” In short, you employ it (though more or less unconsciously) in every thinking process of Deduction, by means of which a decision, or Judgment is reached. If you will take the trouble to analyze any thought leading up to a Deductive Judgment, you will find that each step or stage of the Syllogism has been employed.

But, here is an important point: In ordinary thought and deductive thinking, there is a “slurring,” suppression, or omission from conscious thought of one or more of the three respective Propositions composing the Syllogism. The missing Proposition, however, still exists in the mind of the thinker—in his subconscious or unconscious fields of mentation. They are always “taken for granted” or implied, even though one may not be conscious of their presence. When you analyze even the most informal argument, or simplest deductive inference, you will find that the missing elements are always there “in the mind.” Logicians apply to the results of this “slurring” or “leaving out” process the term, “Enthymeme” (meaning, “in the mind”). You are not required to remember this name, however: you may think of it simply as “A Short-Cut Syllogism”—for that is exactly what it is.

“Short-Cut” Syllogisms vary greatly in particular form, but are reducible to three general classes. Here follow examples of each of the three classes. With Major Premise omitted: “We are a free people; therefore, we are happy.” Here the Major Premise, i. e., “All free people are happy,” is unexpressed, though existing “in the mind.” With Minor Premise omitted: “Poets are imaginative: therefore, Byron was imaginative.” Here the Minor Premise, i. e., “Byron was a poet,” is unexpressed, though existing “in the mind.” With Conclusion omitted: “All braggarts are cowards; Bombastes is a braggart.” Here the Conclusion, i. e., “therefore, Bombastes is a coward,” is unexpressed, though existing “in the mind,” and also probably intended to be called into the mind of the listener or reader.

This last form is often employed very effectively in debate or public speaking. The Frenchman’s characteristic shrug of the shoulders is really a syllogistic “short-cut,” in which the Conclusion is unexpressed in words, though existing “in the mind” and suggested by the gesture. Also, when you say, “I allow you to draw your own conclusion,” you are employing this form of “short-cut”—often quite effectively.

You will find it excellent mental exercise and practice to restore a “short-cut” Syllogism to its original and complete form. Stanley Williams says: “It is one of the finest exercises of the mind that it is possible to employ—an exercise superior even to geometry and other branches of mathematics, because in it we are dealing with the practical everyday inference of our reason.” Such practice will enable you readily to detect fundamental fallacies advanced in the reasoning or arguments of other persons. As an illustrative example of this form of practice we offer the following: “This thing will sink in water, for it is a stone.” Restored to syllogistic form, it is: “All stones sink in water; this thing is a stone; therefore, this thing will sink in water.”

The textbooks of Formal Logic will give you a terrifying list of the numerous forms of Propositions and Syllogisms. This list frequently discourages the practical man, and drives him away from a further investigation of the subject. But inasmuch as all of such forms may be reduced to the few simple forms referred to by us in this section of this book, and inasmuch as the technical distinctions are of very little real practical value to the person who desires merely to become familiar with “the working principles” of Practical Logic, we shall omit further reference to them here. In addition, the textbooks of Formal Logic present a number of highly technical rules which govern the logical forms of the Syllogism; these also we shall omit. With the aid of Common Sense, and a knowledge of the fundamental principles of Practical Logic, one may easily dispense with these hair-splitting distinctions.

There are, however, several basic rules under which Deductive Reasoning must proceed in order to be valid, and which if violated result in fallacy or false-reasoning—this becoming sophistry when deliberately employed to deceive others or one’s self. These basic rules we now ask you to consider; they are as follows:

1. The Terms must be Unequivocal, and not Ambiguous.
2. The Premises must Represent Actual Facts.
3. Particular Terms must not be Employed as Universal Terms.
4. The Conclusion must Contain Nothing which is not Involved in the Premises.

You are now invited to consider carefully the following more detailed statements concerning each of the above-stated general rules of Deductive Reasoning, together with examples illustrating each rule.

1. The Terms must be Unequivocal, and not Ambiguous, i. e., they must be clear, plain, and not employed in more than one meaning or sense. This, because the same term, employed in the same argument in more than one of its meanings, practically becomes two terms, or more; in such case, one Premise may contain the term employed in one sense, while in the other Premise the same term may be employed in another sense, which would result in false reasoning and absurd conclusions. This was a favorite device of the ancient Sophists; it is employed frequently (in more or less involved and disguised form) by many sophistical speakers and writers of our own time and lands. Here is a classical illustration: “A man says: ‘I am lying’; if he is lying, he is telling the truth; if he is telling the truth, he is lying.”

Other examples of Fallacy arising from a violation of this rule follow: “Feathers are light; light is contrary to darkness; therefore, feathers are contrary to darkness.” “No courageous thing flies; all eagles fly; therefore, eagles are not courageous.” “All artists design; all designing persons are untrustworthy; therefore, all artists are untrustworthy.” “Vice ran in the family; the police ‘ran in’ the family; therefore, the police were vicious.” “No cat has two tails; every cat has one more tail than no cat; therefore, every cat has three (i. e., one more than two) tails.” One form of this Fallacy consists in placing the mental or verbal accent or stress upon the wrong term; as for example: “Thou shalt not bear false witness against thy neighbor; all that is not against thy neighbor is for him; therefore, thou shalt bear false witness for thy neighbor.” The above examples, in more complex and subtle form, illustrate the favorite devices of certain sophistical reasoners, debaters and teachers.

Another variety of this form of Fallacy consists of the use of the words “all” or similar terms, in one place as a collective term, denoting “a combined and united whole”; and in another place as a singular term, denoting “any, each, or every single individual or object forming a part of a whole.” Example: The statement that, “Any man can carry away all the sticks in this pile,” (meaning to carry away all the sticks singly, one by one) is far different from the assertion that any man can carry away all such sticks at once, in a single load. Likewise, the statement that “No man can carry away all the sticks in this pile” (meaning to carry them away in a single load), is far different from saying that no man could carry away all of them, one by one. This form of Fallacy is far more common than you might imagine from the above stated simple examples. It becomes more dangerous when expressed in more complex and involved form.

Another variety of the same form consists in confusing the meaning of a grammatical phrase. Example: “The animals walked in two-by-two; two and two make four; therefore, the animals walked in by fours.” “You have said that what you bought in the market yesterday, you ate today; you bought raw meat in the market yesterday; therefore, you ate raw meat today.” “You have said that it is not true that virtue consists of utility; if this be true, then virtue lacks utility; therefore, you hold that utility is a thing lacking in virtue.” “Patriotism is the last rest of a scoundrel; therefore, every patriot is a scoundrel.” Such sophistical quibbles and tricks distinguish shyster lawyers, Smart Aleck debaters, and others of their kind; they are beneath contempt when employed in argument with serious intent— and they are so employed far oftener than you might suspect. Did you ever hear of the shyster who asked the witness under cross-examination, the question: “Have you quit beating your wife?” and insisted upon a “Yes, or No” answer. The man had never beaten his wife: imagine his dilemma!

Another variety of the same class of Fallacy is that in which the principles of a general law are sought to be applied to a particular case in which the circumstances are entirely different. Example: “All who kill are murderers; soldiers kill; therefore, soldiers are murderers.” This sophistry is discovered when one refers to the definition of “murder,” which is: “illegally killing a human being with malice aforethought.” Yet public men of a certain type have sought persistently to perpetrate this sophistry, and thus to influence the public mind in certain directions. Once more: the sophistry that, “In Aesop’s fable the fast hare was beaten by the slow tortoise; of the two horses entered in this race, one is fast, the other slow; therefore, the slow horse should win this race.” Here, of course, Aesop’s tortoise won “in spite of” its slowness, not “because” of it.

1. The Premises Must Represent Actual Facts, i. e., they must represent facts derived from one’s own careful observation and experiment, or from his own logical reasoning; or else from carefully considered and accepted reports of the experiences, observations, or reasoning of others deemed to be capable and in a position to observe, experiment, or reason carefully and correctly, and to judge with logical precision. The importance of this rule becomes apparent when one realizes the truth of the ancient aphorism: “One can prove anything whatsoever, if he be permitted to assume certain Premises; this, without violating a single technical rule of Deduction.” Admitting the Premises of an argument or process of reasoning, the conclusion proceeds certainly, inevitably and invariably to a logical conclusion, without regard to the actual truth of the Premises so employed. But, remember always, that a logical conclusion is never truer than are the Premises from which it is deduced, even though the processes of reasoning or argument be logically perfect. If you start with the Major Premise that, “All White is Black,” you may reason with absolute logical correctness to the Conclusion that, “This is black snow.”

Your Premises must represent correct observation, experiment and the experience of yourself, or of others deemed to be competent authorities. Your own experience must be subjected to logical inspection, and must bear the test of logical Induction and Deduction. The evidence of other persons must be subjected to logical and critical inspection and judgment. The two main factors determining the degree of the validity of this last-mentioned class of evidence are as follows: (1) Ability, and (2) Veracity; but alas! such associated virtues are rare, for some able men lack veracity, and many veracious men lack ability to observe, reason and judge.

Many a “good man and true” lacks critical perception and logical judgment; such a man is particularly dangerous, because his virtue is apt to be mistaken for the ability which he really lacks. Again, a man may be very able in his own particular line of thought and work, but still like a child or a dunce in certain other lines. The man recognized as an “authority” in one line may be an ignoramus in another line; a failure to perceive this has led astray public opinion and personal belief in very many cases, some of which may have come under your own observation. The “authority,” to be valid, must be real and not merely assumed. Common sense must be employed in deciding upon the validity of the opinions of claimed “authorities.” The “authority” should be subjected to the test-question: “How do you know?” You are justified in being “from Missouri” in this respect.

Fallacy of “Begging the Question”: This is quite common, and it frequently deceives even careful persons whose attention has not been directed to the logical principle violated in it. It consists of assuming, “taking for granted” (or asking others to do so) a Premise (usually a Major Premise) which is not based upon logical reasoning or upon actual human experience and judgment.

It is true that “all reasoning or argument must begin with a Proposition not actually proved at the time,” and which is to be “taken for granted” as representing valid human experience and judgment—something which is assumed to be “self-evident,” and requiring no further proof or demonstration. Otherwise, the reasoning process would be like running back along the links of an endless chain; one must begin somewhere. But such “self-evident truth” must really be one based on universal human experience, a well-verified hypothesis, or a valid logical deduction from these; a mere assumption or claim will not answer.

Likewise, it is illogical and contrary to common sense to hold that a Proposition or Premise must be accepted as true and valid until it is actually disproved. The contrary is true: the rule is that “The Burden of Proof” lies upon the person advancing the Proposition; “He who affirms must prove, if called upon to do so.” A favorite device of some debaters, writers of a certain type, and some persons engaged in argument, is to “shift the burden of proof,” and to hold that unless the Proposition is disproved it must be admitted to the argument. The absolute rule is: “The Proposition must be positively proved, if demanded; no mere negative failure to disprove it can constitute or serve as positive proof of the Proposition.”

The Fallacy of “Begging the Question,” is a very common and, often a very dangerous one; it appears in many forms, and under many disguises. It is particularly dangerous, because especially insidious, when it appears in disguised form in the Major Premise; here the formal Conclusion becomes merely an echo or repetition of the original Proposition, the latter being cleverly injected into the argument without being subjected to logical inspection or proof. Once admitted to the argument, the Proposition, thus boldly assumed, becomes the valid basis for subsequent deduction and reasoning of a perfectly logical character. The unsupported Proposition is treated as if it were really the Conclusion of a previous process of syllogistic reasoning; whereas, it really is merely “taken for granted” or assumed without valid basis. In effect, it is really a case of attempting to prove a Conclusion by itself, without the presence of supporting Premises.

Many public speakers commit this fallacy—often quite deliberately. Experience has shown them that usually (in the popular phrase) they “can get away with it.” Aaron Burr illustrated the practice in his celebrated cynical statement that, “Truth is that which is boldly asserted, and plausibly maintained.” Bulwer makes one of his characters, an unusually clever rascal, say: “Whenever you are about to utter something astonishingly false, always begin with: ‘It is an acknowledged fact,’ etc.; or ‘It is admitted by all,’ etc.; or ‘No thinking person denies,’ etc.; or ‘It is a truth undeniable,’ etc.” The same character advises that when one is called upon for the proof of something admitting of no logical proof, he should “look solemn, and, striking his breast, should say: ‘I find it here!’”

Another form of “Begging the Question” consists of the use of “question-begging epithets,” i. e., of terms or epithets suggesting or conveying unpleasant or evil associated meanings, and thus serving to arouse prejudice against, or even to damn the thing, by the use of the epithet or term which really has not been proved to apply to the thing in question at all, and of which the thing is possibly entirely innocent and free. Thus, we often hear arguments in which it is “boldly asserted” (without the slightest proof, be it noted) that such and such an idea is “atheistic,” “anarchistic,” “unpatriotic,” or “immoral”; the audience, bearer, or reader being asked to “swallow whole” without investigation or thought, the idea represented by such terms. It is a case of “giving a dog a bad name” and thus causing him to be stoned to death. Jevons says: “We should always be on our guard against being misled by ‘question-begging epithets’.”

The Fallacy of “Circular Reasoning” is another variety of this general class of Fallacy; like the other varieties and forms, it is quite common, and often is quite dangerous. It consists of, attempting to prove a Proposition by itself; or, proving a series of Propositions one by the other in a Vicious Circle.” In its simplest form it is perpetrated by simply attempting to demonstrate or to prove a thing by means of its own definition, as for example: “Glass breaks because it is brittle; it is brittle because it breaks easily”; or, “We can see through glass because it is transparent; it is transparent because we can see through it”; or “The girl is dumb, because she lacks the power of speech; she lacks the power of speech, because she is mute.” An extension of the false principle is found in arguments or syllogisms in which the Major Premise is merely the unproved Conclusion stated in different terms but having the same essential meaning.

More complex, and consequently more dangerous, forms are as follows: “My Church is the true Church, because it was established by God, and God could have established none other; it must have been established by God, because it is the true Church, and such could have been established by none other than God.” You will notice how convincing this seems at first hearing; but you will perceive that not even a single iota of proof, not even a single trace of logical argument, is offered in the whole statement; there is not even the slightest evidence, proof, or reasoning presented to show any connection between God and the establishment of truth of that particular Church; yet persons are deceived by just such false reasoning concerning many important subjects.

Again: “My political party is honest, because it advocates honest principles; the principles advocated by it must be honest, because they are advocated by an honest party.” Once more: “The Koran is infallibly true, because Allah inspired it; we know that Allah inspired it, because it is so stated in the Koran.” Finally: “The man is truthful, because he states so himself; being truthful, that which he states must be truth.”

Circular Reasoning, however, is most successfully employed in long arguments, where its detection is difficult; while in simpler form the same false reasoning would be readily detected.

Frequently it is perpetrated by the use of synonyms which are suggested and assumed to express more than the original term employed in the Proposition, but which really do not do so. A particularly dangerous and subtle form is that in which as McGilvary says: “There are two or more Syllogisms interrelated in such a way that the Conclusion of each Syllogism is the Premise of some other. In this way, the Conclusion, or what is proved, in one Syllogism is used in another Syllogism as a basis of proof for a Proposition which, in its turn, ultimately comes to be used as a basis of proof for the first Syllogism.” Read over this last statement until you thoroughly understand it; when you are able to do this, you will be prepared to give battle to the Vicious Circle.

• Particular Terms must not be employed as Universal Terms; that is to say, terms denoting only “part” or “some, of a class of things must not be so used that they seem to denote “all” or “the whole” of that class. In order that you may thoroughly understand this rule, we shall now call your attention to the essential distinction between Particular Terms and Universal Terms expressed in the form of Particular Judgments and Universal Judgments, respectively.

Particular Judgments are Judgments which are not general, i. e., which do not include “all” or “the whole” of the class of things to which it applies; but which, instead, include only a part, portion, or “some” of that class—or “at least some” of that class. Particular Judgments are marked by the presence in them of the words, “some,” “certain,” “a few,” “many,” “most,” or similar terms indicating that merely a part, portion, or “at least some” of the entire class is denoted. The terms, “this,” and “these,” also usually denote Particularity but in exceptional cases they are sometimes employed to denote whole classes—exactness of meaning should be ascertained when such terms are employed in forms possible of being interpreted in either way.

Examples of Particular Judgments are as follows: “Some bread is biscuit”; “Certain snakes are venomous”; “Many men are vain”; “Most mules are stubborn”; “A few negroes are albinoes”; “That Virginian is a Republican”; “This Irishman is a Protestant.” When Particular Judgments are announced or employed, they indicate expressly that only a part or portion of a general class is involved in the statement; in them is also implied the fact that “there is something left in the class”

Here, however, is an important point to remember in connection with that implied “something left in the class,” viz., that the remaining portion so “left in the class” may lack the characteristics affirmed of the portion denoted by the Particular Term, or it may not lack them. By employing the Particular term (i. e., “some” or its equivalents) we may mean either (1) that the “remaining or other part or portion” lacks the characteristic in question; or (2) that our certain knowledge of the class extends merely to that particular part or portion indicated by the Particular Term and involved in the Particular Judgment; or (3) that there remains a general doubt or possible indecision concerning the “remaining part.”

The meaning “at least some” covers each and all of the above stated three respective contingencies; therefore, this meaning should always be kept in mind when dealing with Particular Terms or Particular Judgments in Deductive Reasoning.

Universal Judgments are Judgments which are general, i. e., which include the entire class of things to which it applies—all the parts, portions, or individuals in that class, and not merely a part, portion, or “some” of the class. For instance, when we say that “All men are mortal,” we mean that the entire class of “men” possess the characteristic of mortality. Universal Judgments are marked by the presence in them of the words, “all,” “every,” “each,” “any,” “the whole,” or similar terms denoting “all the number or class”; also by “no,” i. e., “not any of the number or class”. Universality either takes in the entire number or class, or else leaves out the entire number or class; the principle is the same in both cases. Examples: “All men are mortal”; “Every dog is an animal”; “Each man was armed”; “Any dog will eat meat”;

“The whole family was present”; or, “No dog is a cat”; “None of the family were absent”; “Not any of the fishes have warm blood.”

Note the following important point: Universality is also sometimes implied and tacitly indicated in certain Particular Terms employed for convenience to denote entire numbers or classes of things, and not merely single individual things. For instance: “Man is mortal”; here the term “‘Man” is employed in the Universal sense and meaning of “All men,” and therefore becomes a Universal Term—the Judgment becoming a Universal Judgment. Terms like “The Horse,” or “The Cow,” etc., or “A Horse,” or “A Cow,” (meaning “any horse” or “any cow”), are also frequently employed in this way; when so employed they become Universal Terms, and mark Universal Judgments. In such cases, the Universality of the Judgment is tacitly indicated, the magic words, “all,”, “each,” “every,” “any,” etc., always being implied. Care must always be taken to determine whether such terms are employed in the ordinary Particular sense and meaning, or, instead, in this special Universal sense and meaning. Many grave Fallacies arise from confusing or confounding Universals and Particulars in this way.

Examples of Fallacies arising from a violation of the rule now under consideration are as follows: “White is a color; Black is a color; therefore, Black is White”: here “Color” is used in its Universal sense of “All Color,” instead of its Particular sense of “some Color.” The same fallacious use of Particular Terms for Universal Terms results in the following several false Conclusions: “All birds are bipeds; no man is a bird; therefore, no man is a biped”; “Some Chinamen are highbinders; this man is a Chinaman; therefore, this man is a highbinder”; “Some Russians are Bolsheviks; Ivan is a Russian; therefore, Ivan is a Bolshevik”; “Biscuit is bread; this loaf is bread; therefore, this loaf is a biscuit”; “Indians are Americans; John Smith is an American; therefore, John Smith is an Indian”; “All thieves are human; the bishop is human; therefore, the bishop is a thief.”

But why multiply examples? The principle is plain, once it is grasped. Once understood, it is seen to apply to countless cases; and is found to be violated in the reasoning and arguments of many persons who should (or do) know better. When used for the purpose of deceiving, it becomes sophistry or casuistry; and it is often so used, particularly by subtle suggestions and in disguised form.

Here is the essential principle: Terms denoting merely “some” must not be used to denote “all.” When we say that, “All dogs are animals,” we do not mean “all animals,” but rather we mean “some animals”—the Particular mark “some” being implied and tacitly indicated. Fully stated, the Judgment or Proposition would be as follows: “All dogs are some animals,” i. e., that all-the-dogs-there-are-in-existence constitute a part, portion, or “some” of the entire class of animals—not “all” or “the whole” of the “animal” class. The implication would be that also there are “some animals which are not dogs,” as well as that “some animals which are dogs.”

The following diagram (with accompanying explanation) will be found helpful in fixing and keeping this principle in your mind. It is based upon the analysis of the familiar “trick Judgment” stated as follows: “Biscuit is Bread, but Bread is not Biscuit.” Analyzed, this Judgment means: “All Biscuit is some Bread; Some Bread is all Biscuit”—with the implication that “There is also some Bread which is not any Biscuit.” Stated more simply, we have: “All Biscuit is Bread; but all Bread is not Biscuit: there is some Bread which is not Biscuit; but there is no Biscuit which is not Bread.”

 

There are three rules governing Deductive Reasoning which are derived from a number of more technical ones set forth in works upon Formal Logic. Practical Logic employs these Derivative Rules, considering them sufficient for its general purposes; these rules are as follows:

1. “One Premise, at least, must be Universal”; this because of the fact that, “From two Particular Premises, no logical Conclusion can be drawn.” An example of the violation of this rule is found in the Syllogism: “Some men are mortal; Socrates is a man; therefore, Socrates is—” What? The only logical Conclusion possible is that “Socrates may be either mortal or not mortal; he must be one or the other; he cannot be both”; but this is no more than the Law of Opposition and Law of Excluded Middle tell us. There is no definite Conclusion possible from two Particular Premises; one Premise, at least, must be Universal.
2. “If One Premise is Particular, the Conclusion also must be Particular”; this because of the fact that, “A Universal Conclusion can be drawn only from two Universal Premises.” Examples: From the Universal Premise, “All birds lay eggs,” and the Particular Premise, “Some animals are birds,” we may logically deduce merely the Particular Conclusion that, “Some animals lay eggs”; but we cannot logically deduce the Universal

Conclusion that, “All animals lay eggs.” But, on the other hand, from the following two Universal Premises, “All finches are birds; all sparrows are finches”; we may logically deduce the Universal Conclusion that, “All sparrows are birds.”

• “The Conclusion must Contain Nothing that is not Involved in the Premises”; this, because, as the Conclusion is necessarily made up of the material of the two Premises, any addition to this material would be an unwarranted and illogical introduction or “dragging in” of foreign matter or extra material which, in the words of “Pooh-Bah” “have nothing to do with the case.” Such foreign matter, thus dragged into the case, is, as the lawyers say, “incompetent, immaterial, irrelevant, and impertinent.” Yet this Fallacy, often deliberately employed as specious sophistry, is frequently perpetrated, and often succeeds in accomplishing its purpose.

The Fallacy consists in the statement ofIrrelevant Conclusions. In one of its phases the Irrelevant Conclusion is caused by the employment of certain terms as Universal Terms in the Conclusion, while in the Premises they were used as Particular Terms; we have already considered this form of the Fallacy. The second phase consists of the introduction into the Conclusion of Judgments entirely foreign and alien to the issue, and which are not in any way logically involved in the Premises. This last mentioned form is sometimes known as “Non Sequitor,” meaning, “It does not follow.” Non Sequitor is marked by: “The introduction or dragging-in of points ‘not at issue’ in an argument or course of reasoning, i. e., points having nothing at all to do with the case under consideration, or points having no possible logical relation to the original Premises.”

Examples follow: “All men are rational; Socrates is a man; therefore, Socrates is truly noble.” “Episcopacy is of Scriptural origin; the Church of England is an Episcopal church; therefore, the Church of England should be supported by tithes.” “The Church is a good institution; the State is a good institution; therefore, the Church and the State should be united.” “The evidence shows that John Smith is a liar; all murderers are liars; therefore, John Smith should be hanged.” “This place is called Stony Stratford; I was never so bitten by fleas in my life as here; therefore, rightly is this place called Stony Stratford.” More cleverly disguised forms of this Fallacy, yet involving the same essential principle, pass muster every day in argument, debate and serious discussion. Remember the adage: “If it does not follow logically from the Premises, it is foreign to the issue.”

A General Fallacy There is another Fallacy frequently appearing in reasoning and argument, but one which is not referred to in the specific Rules of Logical Reasoning. We wish to direct your attention to it: it is known as the Fallacy of Prejudice. It is quite common, and often quite dangerous. You should give it careful consideration and honest thought.

Fallacy of Prejudice. By “Prejudice” is meant: “Prejudgment; unwarranted and unreasonable predilection for or objection to anything; especially, an opinion or leaning favorable or adverse to anything, without just grounds, or before sufficient knowledge.” The common forms of Prejudiced Judgment are as follows: (1) Prejudice in favor of Propositions agreeing with our feelings, emotions, or general “likes”; or against Propositions running contrary to our feelings, emotions, or “likes.” (2) Prejudices in favor of Propositions advanced by persons favorably regarded or liked by us; or against Propositions advanced by persons unfavorably regarded or disliked by us. (3) Prejudice in favor of opinions at present held and previously stated by us; or against opinions at present opposed, and previously disputed by us. Let us consider briefly each of these three forms.

• It is quite difficult to divorce our judgments from our feelings. Our likes, loves and hates tend to prejudice our judgments, and to give us a “mental slant” in the direction of the “like” and against the “dislike.” Bernard Shaw tells us that most of our reasoning consists of either trying to excuse or justify our previous judgments and actions caused by our states of feeling, or else of trying to invent excuses for present or future judgments or actions likewise so caused. Feeling and emotion resemble the tinted glass which colors the rays of the sun which pass through it. Everything we consider is apt to be seen colored in the tints and shades which our feelings have imparted to it. You should ever be on your guard against the interposition of the colored screen between your reasoning faculties and the objects or subjects of logical thought. Strive ever to secure the clear, unimpeded passage of the White Light of Pure Reason; let it shine upon the objects of your thought.
• We find it difficult to give the proper value to an opinion, proposition or judgment announced by a person or persons disliked by us. Likewise, we find it quite easy to place an exaggerated value upon opinions, propositions or judgments announced by those whom we like. Here, once more, Feeling seeks to usurp the office of Reason. Truth is Truth, by whomsoever stated; and Untruth is none the less Untruth even when stated by an estimable person, or one very dear to us. A thing “is, or is not, so,” without regard to our opinion of, or our feelings toward, the person making one or the other of these necessary judgments. It is our business to find out “which is which,” by Reason alone, bidding Feeling to step aside and to “keep its thumb off the scale.” Judgments should stand on their own feet; the crutches of Feeling are not required; they are a sign of weakness on the part of Reason.
• It is characteristic of the human mind to incline to support even the weakest opinion or judgment already lodged in it; and to defend such against the attacks of even the strongest truths and reasons. Even when the conflict is confined to one’s own mind, and no other person is involved in it, this remains true. Even though the preconceived opinion or judgment may have been based originally upon insufficient and unstable grounds of reasoning, the slightest proof and the weakest evidence, nevertheless it often requires the very strongest evidence and proof, the most positive reasoning and most certain logic to cause us to budge an inch from our position. We have said to ourselves that the thing was so; we have expressed the same opinion to others; and to change is akin to “backing down.” The thing may be “a poor thing, but it is our very own”; we hate to part with it—to separate it from us too strongly suggests an amputation or the removal of a mental appendix. It is quite right and proper to “hold fast to our opinion”; but we should be sure that the latter is well grounded in fact, and well supported by logical reasoning. We should endeavor to keep at least a fairly “open mind,” even though we keep a keen-eyed sturdy watchman at the gate.

Some Practical “Points”

We Desire now to call your attention to several common sense, practical general “points” which should prove useful and helpful to you in the task of “making up your mind” concerning various subjects and questions toward which you have directed your reasoning powers and logical thought. Some of these have been expressly stated or else implied in some part of the foregoing instruction; others arise from the experience of men in applying the principles which have been presented to you in these pages. In either case, the present reference is intended to be merely suggestive, not a detailed exposition.

PoiNT I. All logical argument, reasoning, or proof must begin with something necessarily taken for granted, admitted or accepted as self-evident and axiomatic; or else “assumed for the sake of the argument,” and accepted tentatively in order to permit the argument, discussion or reasoning to begin. Without such a starting point, there can be no reasoning, argument or discussion on any subject whatsoever; an effort to find the ultimate and fundamental proof, fact or truth in any case will be endless, for the chain must be endless so far as we are concerned, inasmuch as there is a limit to our respective lives, while there is apparently no limit to such backward tracing of Conclusions to their Premises, these to preceding Conclusions and their Premises, and so on, and on, ad infinitum. If we are to begin at all, we must begin somewhere; and that position of “somewhere” always is occupied by a Something or Somewhat which must be accepted, admitted, or assumed as a basis, and which must be “taken for granted” at least tentatively. This Something or Somewhat is usually known as “the first principle” of the argument, discussion or reasoning.

Point II. There can be no logical argument or discussion between persons who do not accept the same “first principles,” at least tentatively; neither can there be logical reasoning on the part of the individual who does not accept some “first principle,” at least tentatively, in order to think intelligently on any subject whatsoever. A realization of the fact would prevent much futile argument and discussion, and much purposeless and inconclusive reasoning.

Point III. The “goodness” or “badness” of a condition, action or belief may be determined only by first agreeing upon its associated object, purpose, end or effect. It is impossible to determine whether or not a thing is “good,” unless we first ask and answer the question, “good for what?” This brings a realization that most so-called “good” or “bad” is purely relative; that what is one man’s good, is another man’s bad. The rain that is welcomed by farmers in one section is dreaded by those in another; a rise in the market makes some men rich, while ruining others; the point of view of the average practicing physician or undertaker must of necessity be entirely different from that of their sought-for and desired patrons. There must be an accepted standard—a stated “good for this, or because of that.”

Point IV. The old proverb, “De gustibus non est disputandum” (i. e., “There is no disputing about tastes”) expresses a truth which, if generally recognized, would prevent much futile argument and discussion, and save much fruitless reasoning.

Without a standard, arguments of this kind are without end. To each person his own taste is a standard, in absence of the acceptance of a higher one. As a writer has said: “Tastes differ so much among individuals, nations, or in different ages that it is utterly impossible to set up a standard of taste applicable to all men and to all ages of society.”

Not only are there countless individual preferences in taste, but there are also local standards generally accepted as authoritative, and there are even passing fashions of taste in all communities. There are two general forces at work in setting standards of taste: the current standards result from a balance between these two. These two factors are (a) the numberless individual tastes caused by the temperaments, education, or associations of the different persons, and (b) the comparatively uniform standards of taste adopted or accepted by the majority of the most intelligent and cultured persons in any community at any given time. But in any case, there can be no logical discussion or argument concerning Taste, unless some certain or general standard be accepted or assumed at least tentatively.

PoiNT V. Likewise, there can be no logical argument or reasoning concerning the subject of the merits or demerits of particular or general behavior, unless a definite, certain standard of conduct and behavior be accepted, adopted, admitted, or assumed at least tentatively, by the reasoning person or the parties to the argument. This standard may be “the law” of that time and place; the accepted common general rule of good behavior and conduct—the accepted customs—of that time and place; the accepted principles of ethics of the best thought of that time and place or the moral codes, commandments, or teachings of some particular accepted religion.

The religious standards, for instance, may consist of the Ten Commandments; or of Christ’s Two Commandments; or of the Golden Rule; or of the Sermon on the Mount; or of the teachings and rules of the Church: in other lands, this being true of the particular religions accepted and at least nominally followed by the people of the land. The legal standards are set by the respective laws of the states or countries in question. The general moral standards are represented by the customs and habits of the best part of a community. The modern ethical standards are represented by the following statement of Professor Davidson: “It is not enough for a man to understand the conditions of rational life in his own time. He must likewise love these conditions and hate whatever leads to life of an opposite kind. This is only another way of saying that he must love the good and hate the evil; for the good is simply what conduces to rational and moral life, and the evil simply what leads away from it.”

But, whatever may be the standard adopted, accepted or assumed, there must be some such standard, else all argument, discussion or reasoning on the subject must be futile, meaningless, and endless.

Point VI. Reasoning and argument about the nature and characteristics of things in general, or in particular, should always be conducted on the basis of “things as they are,” rather than upon “things as they ought to be.” The “ought to be” question is quite proper in its place—but its place is “some other place”; it has no place in the thought concerning the nature, characteristics, and present state or conditions of the thing or things in question. A failure to observe this precautionary measure is the cause of much futile and endless discussion, and of much muddled thinking. Nature, Life, Society, and Things in general, must first be known “as they are,” before any improvement or progress is possible. We must know “what things are, and how they behave:” before we can reason out possibly better ways. Many persons shrink from seeing “things as they are” in Nature—they are afraid to look facts in the face; they are afraid of “the naked Truth,” evidently considering it “un-nice,” if not, indeed, actually indecent.

Your Premises should be: “All A is B,” or “This A is a B” (if such be the case), rather than “All A should be C” or “This A should be a C”—that is, if you are arguing or reasoning about the nature of, or the truth concerning the thing in question, or of the present facts of the case. The “should be” or “ought to be” or the “it is a pity that it is not,” is quite another matter; such requires a new Premise, involving an entirely different line of argument or course of reasoning. In logical reasoning, the scientific spirit, not that of the sentimentalist, should govern. This is not asking too much of you: if Omniscience sees and knows everything, then it must see and know things “as they are”—you are merely asked to endeavor to follow the same course to the best of your ability.

Point VII. You will do well to realize and recognize that “everything has its opposite”; that there are always “two sides to every question”; that most statements of truth are merely half-truths, the other halfbeing left unstated; that Truth is usually discovered “in the middle of the road,” or to be the Golden Mean between the two extremes. Truth usually is found to consist of a reconciliation of the “opposites”; or the harmonization of the two “opposing” (but not really “contradictory”) aspects of the case. In most cases it will be found that neither “All A is B,” is true; but that the truth is that “Some A is B, and Some A is not B.” Consequently, when you encounter a case in which each of the two sides has many capable adherents, and each is well supported by fact and argument, you may be reasonably sure that the whole truth lies in between the two extremes, and may be found by reconciliation and “a broader and deeper solution.” There formerly raged a violent dispute as to whether Heredity or Environment is the prepotent factor in shaping character; much was said on each side, and each side arrayed strong facts to support it. Then, along came Herbert Spencer with his “deeper and broader solution” that Heredity is merely the results of past Environment, and that present Environment is merely Heredity “in the making.” Likewise, the same gifted philosopher harmonized the old dispute between the adherents of Intuition (of a certain kind) and those of Experience regarded as the basis of certain “universal notions”; he showed that such universal notions might be called Intuitive, but that this Intuition originally arose from the actual experience of the race, and in time, through inheritance, become fixed in the race as “necessary beliefs.”

All this brings us to a realization that, as a writer has said: “Anything may be defended by logical argument or reasoning that does not involve a logical contradiction in terms,” i. e., that does not conflict with the universal Laws of Thought which we have presented to you in this instruction.

Point VIII. Much attention of late years has been given to the Pragmatic aspect of things—to the aspect of Practical Use and Utility. The Pragmatic test, i. e., How will it work? What will it do? What use is it?” is now being applied in every field of human thought, every branch of study, every important question of Judgment and of Logical Reasoning. There is in the air of the times a disposition to demand of everything the answer to the great question: “What of it?” (You will remember the three questions suggested by us to you in a preceding part of this instruction, viz., “What is it? How do you know it? What of it?—this last is the Pragmatic factor.) There is found a strong tendency on the part of modern writers and teachers on the Art of Thinking to advise that one should not waste time and effort on reasoning which “leads nowhere,” and which is purely academic in character—”scholarly but not scientific”; but should confine one’s thought to practical questions admitting of definite answer and practical, useful application.

A writer voices this bluntly as follows: “Put away from you all questions which do not admit of a definite answer; and also those of which the answers can have no practical meaning, importance, service or use to you.” Henry Hazlitt states this idea with more gentleness, as follows: “The Pragmatic method can be applied with profit to nearly all our positive problems. Before starting to solve a question—while deciding, for instance, on the validity of some nice distinction in Logic—we should ask ourselves, ‘What practical difference will it make if I hold one opinion or the other? How will my belief influence my action?’—(using the word ‘action’ in its broadest sense). This may often lead our line of inquiry into more fruitful channels, keep us from making fine but needless distinctions, help us to word our questions more relevantly, and lead us to make the distinctions where we really need them.”

Point IX. We have at different points in this instruction pointed out to you the fact that the best reasoning, the truest reasoning, is “purposive reasoning.” In fact, it is not too much to say that there is no real or true reasoning that is not reasoning with and for a purpose. That purpose is the discovery of truth— the answer to a particular or general question. The clearer that purpose, the more clearly understood that question, then the truer, clearer, more definite, and more effective will be the reasoning process. As Hazlitt says: “We cannot think on ‘general principles.’ To try this is like attempting to chew laughing gas. To think at all requires a purpose, no matter how vague. The best thinking, moreover, requires a definite purpose, and the more definite this purpose the more definite will be our thinking. Therefore, in taking up any special line of thought, we must find just what our end and purpose is, and thus get clearly in mind what our problems are. * * * Our first step is to get our problem or problems in mind, and to state them as definitely as possible. A problem properly stated is a problem partly solved.”

Our problems necessitating our reasoning are questions— questions demanding an answer. Our business is to clear away the non-essential elements of the question, and to reduce it to its simplest, most fundamental and basic, essential elements. You should ask yourself: “Just what is the nature of this question; and just what must be the nature of the answer when found?” The analysis required for this reduction of the question to its simplest essential elements, and for the perception of the necessary general character of the sought-for answer, will in itself set you well on your way in your process of reasoning out that answer. Sometimes the careful examination of the “opposite side” will clear away much obstructing material; the analysis of the elements of the thing sought to be avoided, or of the elements of your ignorance, will often point directly and unerringly to the solution. Hegel was quite right in his doctrine that a thing can be fully known only by also fully knowing its opposite.

In beginning your reasoning, carry in mind the homely aphorism of the old hunter, i. e, “When you start out to hunt anything, be sure you know just what you’re hunting—or else you mightn’t recognize it when you run across it.”

Point X. The best thinkers have found an important working principle to consist of the “breaking-up method,” i. e., the method of dividing, or breaking-up the subject of thought into convenient classes, divisions, or parts—each of these being handled in turn by the mind. Logical division and analysis should be followed in the “breaking-up,” in order that the best results may be obtained. The rule of the “breaking-up” should be: Logical Order; Definiteness; Utility.

Jeremy Bentham, though not the originator of this method, was one of its most able practitioners; it has been claimed that “the secret of his strength and originality of thought lay in this method.” John Stuart Mill, in one of his essays, directed attention to Bentham’s use of this method, of which he said: “It may be shortly described as the method of detail: of treating wholes by separating them into their parts; abstractions by resolving them into things; classes and generalities by distinguishing them into the individuals of which they are made up; and breaking every question into pieces before attempting to solve it.”

Hazlitt says: “The systematic thinker is careful of the manner in which he marshals his difficulties. He knows that certain problems should properly be considered before certain others, and he saves himself labor and sometimes error by considering them in that order. * * * Knowledge furnishes problems, and the discovery of problems itself constitutes an intellectual advance.

Whenever you are thrashing out a subject, write down every problem, difficulty and objection that occurs to you. When you get what you consider a satisfactory solution, see whether or not it answers all of them.”

Concluding Advice

You are advised to observe the following general rules in your reasoning, arguments, and discussions. Most of these points have been referred to, or else stated, in the foregoing instruction:

• Define and understand your principal terms, and demand the same of your opponent.
• Be certain of the Premises employed; beware of Begging the Question, and of allowing your opponent to do so.
• Proceed logically, observing the Laws of Thought rationally interpreted; and insist upon your opponent doing the same.
• Avoid prejudice, and unwarranted preconceived opinion; but respect your own opinions, and do not discard them unless better are obtained.
• Understand and observe the distinction between Particular Judgments and Universal Judgments; and be on guard against confusing or confounding them, on your own part and that of your opponent.
• Admit, and permit, nothing in the Conclusion which is not involved in the Premises.
• Apply always (to yourself and to your opponent) the leading questions: “What is it? How do you know it? What of it?”

An observance of the ten general points set forth in the foregoing pages, and of the several general rules briefly stated above, will serve to furnish you with what a writer has expressed as: “An equipment of tests and requirements which would save many people from wasting their time and thought upon discussions, arguments and reasoning, of which they realize neither the origin nor the end.”

The Master Formula In your task of attaining efficient Reasoning Power, you will be aided by a study and the observance of the principles of the Master Formula of Attainment which forms an important element of our instruction. The Master Formula, precisely stated, is as follows: I. Definite Ideals; II. Insistent Desire;

1. Confident Expectation; IV. Persistent Determination; V. Balanced Compensation. Reduced to popular terms, it reads: “You may have anything you want, provided that you (1) know exactly what you want, (2) want it hard enough, (3) confidently expect to obtain it, (4) persistently determine to obtain it, and are willing to pay the price of its attainment.”

 

The End